ФИЗИКО-ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕЗОСКОПИЧЕСКОГО ПОДХОДА К ИЗУЧЕНИЮ ПОЧВЕННО-КЛИМАТИЧЕСКИХ ЗАКОНОМЕРНОСТЕЙ
А.В. Чичулин 
Адрес: ФГБУН Институт почвоведения и агрохимии СО РАН, проспект Академика Лаврентьева, 8/2, г. Новосибирск, 630090, Россия
Цель исследования. Критически проанализировать практику применения системного подхода в почвоведении и выявить существующие проблемы; рассмотреть познавательные возможности микро- и макроскопических подходов при моделировании почвенно-биоклиматических закономерностей.
Методология. Математическое моделирование.
Основные результаты. Предложен новый мезоскопический подход к изучению структуры почвенно-биоклиматических ареалов. Его основу составляют два принципа, названные в работе принципами инвариантности и оптимальности, позволяющие выразить искомые закономерности в форме единой, универсальной, количественной зависимости. Показано, что в математической модели, построенной на основе этих принципов, естественным образом возникают новые, обобщенные понятия, логически объединяющие ранее считавшимися разрозненными, понятия гидро - и терморядов В.Р. Волобуева, коэффициента увлажнения Высоцкого - Иванова и радиационного индекса сухости М.И. Будыко. Кроме того, понятия, детализирующие показатель полноты использования радиационной энергии в биогеоценозе − взаимосвязанные коэффициенты полноты использования тепла и осадков в почвах. Показано, что эти коэффициенты имеют специфические значения для разных почвенно-биоклиматических ареалов. На основе новых показателей проведена группировка почв, отличающаяся в существенных деталях от традиционной.
Заключение. Сделан вывод о том, что новые понятия представляют из себя единую, целостную систему, а подход в целом может быть отнесен к альтернативному физико-теоретическому направлению, в рамках которого природные закономерности описываются экстремальным (вариационным) способом.
Ключевые слова:
принципы симметрии; принцип оптимальности; системный подход; гидротермические коэффициенты; идеализации; математическая модельЦитирование: Чичулин А.В. Физико-теоретические основы мезоскопического подхода к изучению почвенно-климатических закономерностей // Почвы и окружающая среда. 2020. Том 3. № 2. e116. 10.31251/pos.v3i1.2.116
Введение
Одна из поразительных особенностей природы − многообразие возможных схем ее истолкования. Мне это всегда представлялось загадкой. Я не понимаю, почему правильные законы физики допускают такое огромное количество разных формулировок
Р. Фейнман. Характер физических законов
Современное понимание организации сложных природных систем, включая почвы, опирается на представление об их иерархическом строении. Структурные уровни от низших к высшим различаются не только степенью сложности, но и действующими в них закономерностями и, в общем случае, требуют для своего описания различных наборов переменных. Однако, помимо очевидной сложности изучения таких систем, в иерархичности их пространственно-временной и энергетической структуры кроются и возможности их познания. Дело в том, что иерархическое строение позволяет упрощенно представить единую систему как состоящую из нескольких, более простых подсистем, и по отдельности изучать ее с совершенно различных − микро- или макроскопических позиций (Гладышев, 1988). Однако полное системное понимание иерархического объекта требует логического согласование результатов всех подходов, поскольку каждый из них в отдельности является только определенным приближением, имеет пределы своих познавательных возможностей, или, как образно выразились Г. Николис и И. Пригожин (1990), "видит реальный мир лишь через окошко конечной ширины". Это согласование может быть осуществлено различными способами − либо попыткой объединить приближенные результаты, полученные при макро- и микроскопическом подходах, либо новой формулировкой задачи, с самого начала рассматривающей макро- и микроуровни объекта исследования в качестве единой системы.
В настоящей работе реализован второй вариант решения задачи − в ней излагаются теоретические основы нового, мезоскопического подхода к изучению структурной организации почвенно-климатических ареалов, который, в определенном смысле, рассматривает свойства и закономерности почв в приближении, промежуточном между макроскопическим и микроскопическим. С методологической точки зрения, оперируя одновременно переменными, относящимися к микро- и макроуровню описания сложной системы, мезоскопический подход обладает преимуществом в тех случаях, когда различные уровни настолько сильно взаимодействуют друг с другом, что их строгое разделение осуществить нельзя. Объединяя определенные преимущества микро- и макроскопических подходов, мезоскопический подход оказывается в состоянии получить новые результаты, которые иным способом получить было нельзя.
Поскольку описываемый подход, по сути, является физико-теоретическим и связан с неизбежными математическими выкладками, то для облегчения их понимания вопросы методологического обоснования подхода, методических приемов построения математической модели и интерпретации конечных результатов рассмотрены параллельно на качественном уровне и по возможности подробнее. Там, где это представлялось необходимым, теоретические вопросы изложены на фоне исторического контекста, а именно развития методологических и методических проблем почвоведения.
В работе особое внимание уделено изложению "генезиса" и результатам применения мезоскопического подхода. В частности, как путем последовательных трансформаций макроскопического подхода можно добиться снятия его ограничений и в конечном счете придать ему обобщенную математическую форму, которая окажется способной к решению новых, более глубоких задач. А также, как в процессе построения математической модели естественным образом возникают новые понятия, выясняются новые закономерности и формулируются новые принципы.
Предистория
Формирование теоретических основ научных направлений, изучающих иерархические объекты, на начальных этапах развития связывали почти исключительно с редукционистскими тенденциями, с пониманием того, что объективные характеристики "высших" уровней системы не могут быть получены, если не исследованы универсальные законы поведения элементов "низших" уровней. Предполагалось, что эти законы могут быть изучены на изолированных элементах. Стремление понять свойства целого путем изучения его изолированных частей дополнялось неизбежным предположением, что аддитивной суперпозицией их функционирования можно будет объяснить внутренний механизм, управляющий поведением целостной системы (Абрамова, 1978). Для определенных условий такие предположения оказались обоснованными и приводили к разумным результатам. Однако по мере накопления конкретных знаний приходило понимание того, что всякая материальная система своим устройством и внутренними связями накладывает определенные ограничения на проявления универсальных законов природы, справедливых для каждого элемента по отдельности, и порождает дополнительные, нелинейные, системные связи, которые не вытекают из общих законов природы, хотя и не противоречат им. Таким образом, научное мышление постепенно осознавало необходимость, наряду с движением по пути редукции, одновременно воспроизводить и закономерности целостных, многоуровневых структур и, с этой целью, разрабатывать подходы, получившие впоследствии названия холистических, системных, эмерджентных, системно-структурных и т.п.
В почвоведении экспериментальное изучение и простейший теоретический анализ отдельных почвенных свойств и элементарных почвенных процессов, протекающих на нижних иерархических уровнях структурной организации почвы, имеет давнюю традицию. Можно с уверенностью утверждать, что были достигнуты серьезные успехи в изучении и математическом моделировании отдельных физических, химических, физико-химических процессов, протекающих на уровне почвенных горизонтов (Пачепский, 1990; Глобус, 1983). Однако уже задачи теоретического описания движения почвенной влаги, потребовавшие умения решать нелинейные дифференциальные уравнения в частных производных, а тем более описание совместного внутрипочвенного процесса тепло-влагообмена с помощью систем таких уравнений, недвусмысленно обозначили предел применимости простейших методов в физике почв и существенным образом изменили традиционный характер исследования. Первенствующее значение получили численные методы решения сложных почвенных задач. Однако аналитическое и численное решение далеко не равноценны. Ряды чисел, получающихся как результат численного решения, выражая большой объем полезных знаний, не определяют внутренних связей, характеризующих исследуемую задачу, а потому не достаточны для определения общих закономерностей (Гухман, 1973). Вычислительная мощь современных компьютеров не смогла заменить прозрачную смысловую ясность простых линейных закономерностей. Хотя автор уверен, что неподготовленность почвоведов en masse к применению численных методов поспособствовала этому не в меньшей степени. Тем не менее, независимо оформилась своеобразная область компенсации, занимающаяся применением и развитием методов обобщения эмпирических результатов – теория подобия и размерности. По нашему мнению, эта теория представляет чрезвычайно важное и перспективное направление для всего почвоведения, хотя в настоящее время она ограничивается в основном рассмотрением вопросов, традиционно относящихся главным образом к физике почв, а именно − гидро- и теплофизическими, а также физико-механическими свойствами почв (Мичурин, 1975; Онищенко, 1988; Усков, Моисеев, 2018; Глобус, 1987).
Проблематичной оставалась возможность не только решения, но даже постановки подобных задач для процессов, протекающих на высших уровнях, т.е. на уровнях почв и почвенного покрова. А ведь именно на этих уровнях формируются почвенные закономерности, вызывающие наибольший интерес почвоведов. Было ясно, что учитывая представление генетического почвоведения о почве как системе с бесконечно большим разнообразием внутренних и внешних связей, имеющих сложную многоуровневую структурную организацию, возможность довести решение такой задачи до конца в аналитической форме, оставаясь при этом на позициях микроскопической физики, может быть реализована только ценой существенных упрощений − различного рода идеализаций и абстракций. Но упрощение задачи имеет предел, за которым теряется истинное подобие принятого приближения к реальному объекту. За этим пределом полученные результаты в лучшем случае могут носить характер только приближенной оценки, в худшем случае − окажутся неправильными по существу и явятся источником глубоких заблуждений (Гухман, 1973; Седов, 1981). Поэтому на практике до сих пор приходится ограничиваться эмпирическими методами, дополненными либо установлением формальных корреляций между почвой и климатом в частных случаях, либо записью громоздких "экологических матриц" (Соколов, 2004).
Несколько слов скажем о динамических математических моделях, которые с полным правом претендуют на использование системного подхода к изучению продукционных процессов в связи с почвенными режимами. Их с определенными оговорками можно отнести к моделям микроскопического уровня, пытающимся с помощью компьютерных технологий связать микро - и макроскопический уровни. Этот подход обладает как своими достоинствами, так и очевидными недостатками: только для своего описания они требуют несколько сотен страниц (Гильманов, 1978; Полуэктов, 2006; Сиротенко, 1981). У этих моделей свои задачи, требующие отдельного рассмотрения. Мы их специально не рассматриваем, хотя и упоминаем для сохранения полноты и общей логики изложения.
Для лучшего понимания разницы между существующими микроскопическими, мезоскопическими и макроскопическими подходами, их ограничений и преимуществ, на качественном уровне опишем специфику всех подходов более подробно.
Традиционный микроскопический подход к моделированию внутрипочвенного тепло-влагообмена предполагает, что нам известны и строение почвенного профиля и свойства всех генетических почвенных горизонтов. Математическое описание внутрипочвенного тепло-влагообена включает в себя решение системы двух взаимосвязанных дифференциальных уравнений в частых производных, с заданными граничными и начальными условиями, а также тепло-гидрофизических и перекрестных коэффициентов для каждого условно однородного почвенного горизонта. Результатом расчетов является динамика температурного и влажностного полей по всему почвенному профилю за определенный промежуток времени. Из этой динамики гидротермического поля по определенным правилам составляются интегральные эмпирические параметры (например − суммы температур выше 10 ОС). Эти параметры и ставятся в соответствие тому почвенному типу, на примере которого апробировалась модель. Заданные гидро- и теплофизические коэффициенты характеризуют породу как фактор почвообразования, а результирующие температура и влажность − породу и климат вместе. Такой подход удовлетворяет требованиям структурно-системного подхода, но в настоящее время из-за сложности является скорее уникальным исследовательским методом, чем повседневным рабочим инструментом для большинства почвоведов. Потому в настоящее время динамика гидротермического поля почв в подавляющем большинстве случаев изучается экспериментально.
Существующий макроскопический подход изучения почвенно-климатических закономерностей опирается на гидротермические коэффициенты, которые по предположению должны отражать корреляцию между типами теплового и водного режимов и закономерностями распространения почв на земной поверхности. Было предложено несколько гидротермических коэффициентов, представляющих собой различные эмпирические комбинации средних температур воздуха и осадков. Рассмотрим два из них, для которых ниже установим асимптотическую связь с теоретической моделью, разработанной в рамках мезоскопического подхода.
Безразмерный коэффициент увлажнения Высоцкого-Иванова
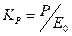
(1)
показывает в какой мере выпадающие в данном регионе осадки возмещают испаряемость и получается от деления среднегодовой суммы осадков Р [мм] на возможную испаряемость с водной поверхности по эвапорометру Е0 [мм].
Безразмерный радиационный индекс сухости Будыко
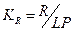
(2)
отражает возможность накопления влаги при данных условиях и определяется как отношение между радиационным балансом территории R [ккал см-2 год] и годовой суммой осадков Р, выраженной в калориях скрытой теплоты парообразования, где L [кал см-3] − скрытая теплота парообразования, для определенности принятая в работе равной 600 [кал см-3] = 0.06 [ккал мм-1] (Реймерс, 1990).
Обратим внимание, что в обоих определениях используется понятие потенциально-возможной величины: в одном случае − испарения с водной поверхности, во втором случае - испарения всех осадков. В этом и заключается основная претензия к этим коэффициентам − они характеризуют не процессы, протекающие в почве, а процессы, протекающие в атмосфере. (Забегая вперед, подчеркнем, что в этом же заключена и потенциальная возможность их обобщения, которая и привела в конце концов к развитию мезоскопического подхода, являющегося главной целью настоящей работы). Другими словами, эти два коэффициента, действующие в рамках макроскопического подхода, характеризуют факторы, не взаимодействующие с почвенным субстратом. На эту особенность коэффициентов мы обратили внимание на качественном уровне. Но, даже с чисто количественной точки зрения, упомянутые гидротермические коэффициенты должны восприниматься критически. Действительно, испарение − это процесс, в котором взаимодействуют радиационный баланс и осадки, но в атмосфере этот процесс протекает иначе, чем в почве. Поэтому, если эти гидротермические коэффициенты рассматривать как количественную характеристику внутрипочвенного взаимодействия тепла и влаги, то следует признать, что они дают приближенную и искаженную картину.
Ситуацию с гидротермическими коэффициентами можно охарактеризовать двояко. С точки зрения микроскопического подхода, учитывающего внутрипочвенные свойства, гидротермические коэффициенты (1) и (2) не являются системными показателями. В системе "почва - атмосфера" они даже не являются граничными условиями. С точки зрения макроскопического подхода эти понятия можно рассматривать как системные, но основанные на грубых допущениях в отношении почвы. Макроскопический подход рассматривают почву как бесконечно тонкую пленку, свойства которой не влияют на процесс испарения ни осадков в воздухе, ни воды с поверхности водоемов. Процессы, описываемые радиационным балансом и осадками в такой почве, не взаимодействуют не только с почвой, но и друг с другом. Потому в географическом отношении коэффициенты (1) и (2) отражают не почвенно-климатические взаимосвязи и закономерности, а лишь потенциальную пригодность для почвообразования климатических условий. Глубокое теоретическое понимание этих взаимосвязей заменяется на формальное установление корреляций, онтологический смысл которых объясняется "дополнительным" к корреляциям словесным описанием. Можно утверждать, что макроскопический подход в целом, сохраняя математическую простоту, в своей основе содержит сильные идеализации и в этом отношении условно может быть назван грубым.
Сделаем оговорку в связи с использованием понятий грубый, детальный, микро-, мезо-, макроскопический и т.п. Эти понятия являются соотносительными, зависят от контекста и не претендуют на абсолютный смысл. Микроскопический подход в одной задаче может рассматриваться как мезо- , а в условиях другой задачи как макроскопический.
Резюмируя, можно утверждать, что внутрипочвенные свойства и гидротермические коэффициенты с формально-математической точки зрения, являются понятиями, относящимися к разным, напрямую не связанным, иерархическим уровням понимания почвенно-климатических взаимосвязей. И простым перечислением переменных, относящихся к разным уровням, задача не решается. Но реальная-то связь между климатом и почвенными свойствами существует. Поэтому продолжает оставаться актуальным методологический и теоретический вопрос: в каких понятиях должна отображаться эта связь, если гидротермические коэффициенты могут отражать ее лишь грубо и формально?
Сформулированный вопрос приводит к необходимости разработки нового, в определенном смысле "промежуточного", мезоскопического физико-теоретического подхода, который, сохраняя простоту макроскопического подхода, более детально может описать процесс взаимодействия климатических факторов и почвы. Такой подход должен удовлетворять ряду условий:
- базироваться на фундаментальных методологических принципах;
- оставаться достаточно простым в математическом отношении;
- не переступать красную черту "переупрощения";
- описывать процессы, протекающие на высших уровнях организации почвы;
- выражать почвенно-климатические закономерности в явном, аналитическом виде.
Оправданием модели, построенной в рамках этих жестких, и даже на первый взгляд взаимоисключающих ограничений, должны быть присущие ей функции полноценной теории: объяснительные, прогностические, способность давать новые результаты.
Критический анализ применения системного подхода в почвоведении
При теоретическом рассмотрении иерархических систем возникает необходимость одновременно работать с переменными, относящимся к разным уровням. Закономерности, действующие в таких системах, отличаются от закономерностей одноуровневых систем. Поэтому необходимо ясное понимание методологических и методических особенностей изучения подобных объектов исследования и общих следствий, вытекающих из них. Методология системных исследований содержит инструментарий, необходимый для рефлексивного осмысления исходных посылок изучения таких систем, а также для выработки адекватного им формального аппарата (Дружинин, Ванярхо, 1989). Рассмотрим и критически оценим некоторые связанные с этой проблемой вопросы, так или иначе затрагиваемые в почвоведении.
Начнем ab ovo. В литературе, посвященной системным исследованиям в почвоведении, популярна точка зрения, что системный подход, широко распространившийся в науке и технике лишь во второй половине 20 века, был заложен в основу генетического почвоведения работами В. В. Докучаева еще в конце 19 века и развит в дальнейшем его учениками и последователями (Добровольский, 2005). С этим можно согласиться лишь отчасти. Дело в том, что на качественном уровне системные идеи возникли еще во времена Древней Греции и были достаточно подробно проанализированы в философских системах Платона и Аристотеля (Агошкова и др., 1998). В дальнейшем, начиная с И. Ньютона, каждая фундаментальная физическая теория, хотя это специально и не провозглашалось, разрабатывалась как конкретная реализация системного подхода. В принципиальном отношении В. В. Докучаев не был первооткрывателем системного подхода как самостоятельного философско-методологического направления. Он не провозглашал его развитие, он пользовался естественным для всех естествоиспытателей стремлением искать взаимосвязи между природными феноменами. Как задолго до него и после него, для ученых, например для физиков, было совершенно естественным искать взаимосвязи между влияющими друг на друга, ранее считавшимися противоположностями − пространством и временем, волнами и частицами, устойчивыми и неустойчивыми движениями. Электродинамика, теория относительности, квантовая механика и др. − их все можно назвать физическими системными теориями. Вряд ли все эти физические теории достигли громадных успехов потому, что физики осознали глубокий, мистический смысл системного подхода и выбрали его в качестве руководящей идеей с самого начала. С большим основанием можно утверждать обратное. Во всяком случае, в физике руководящая роль системного подхода никогда специально не провозглашалась, хотя, по сути, всегда использовалась. Системный подход развился как философско-методологическое обобщение результатов всех наук, почвоведения в том числе. В качестве примера, напрямую относящегося к нашей теме, можно привести классическую термодинамику открытых систем, принципиальные идеи которой Л. фон Берталанфи, считающийся основателем системного подхода, напрямую положил в основу своей общей теории систем (Садовский, 1974). Что касается придания такой большой роли формальной связи "В. В. Докучаев − системный подход", то это заслуга не В. В. Докучаева, а скорее его современных интерпретаторов.
В замечательной работе Т. Г. Гильманова (1978) практически на первой же странице встречаем широко известную цитату В. В. Докучаева о "генетической вековечной и закономерной связи между ... мертвой и живой природой, изучение которой составляет высшую прелесть естествознания". Но тут же читаем: "Почему же в первой половине ХХ века, несмотря на все расширяющееся понимание необходимости целостного, интегрального подхода к изучению сложных систем, не было сделано крупных успехов в синтетическом, количественном изучении сложных динамических систем"? В начале 70-х гг. ХХ века Т. Г. Гильманов видел причину этого в отсутствии соответствующей вычислительной техники. Забегая вперед, предлагаем сравнить это обоснованное мнение с более поздним, не менее обоснованным, но прямо противоположным мнением, высказанном О.Д. Сиротенко о состоянии дел во второй половине ХХ века. Оно приведено в конце данного раздела, со ссылкой на А. Г. Топаж (2014).
Но гораздо более важным, чем вопрос приоритета, является вопрос: в какой степени системные идеи реально используются в современном почвоведении? С нашей точки зрения, зачастую преобладает скорее "системное" терминотворчество, чем реальное методологическое осмысление этого вопроса. Интерпретация системных результатов, теоретическое анализ используемых теоретических методов, обсуждаются крайне робко и привлекают внимание в несравненно меньшей степени, чем это диктуется потребностями почвоведения. А здесь много нерешенных вопросов, в которых следует разобраться, поскольку они оказывают влияние на стратегию его развития как науки.
Даже если рассматривать системные идеи В. В. Докучаева в почвоведении как безусловно революционные и концептуально новые, является фактом то, что не во всех направлениях развития почвоведения они привели к развитию принципиально новых системных идей и методов исследования. Задача о почвенно-климатических закономерностях из их числа. Выше мы уже упоминали, что без критического анализа продолжают использовать простейшие, не относящиеся непосредственно к почвам, гидротермические коэффициенты, многим из которых более 100 лет (Чичулин, 2019). И дело, разумеется не в их возрасте, а в не разработанности методологических и теоретических вопросов оперирования с переменными, относящимся к разным иерархическим уровням описания почвы. В некоторых работах, ссылающихся на эти коэффициенты, только декларируется, что используется системный подход. На практике решения задач во многих случаях ищут и получают только на уровне либо констатации эмпирических фактов, либо установления формальных корреляций, поэтому упоминание "системного подхода" не оказывает ни положительного, ни отрицательного влияния на результат, а является скорее данью "системной" моде.
Например, при анализе интересующих нас работ в направлении, называемом сейчас энергетикой почвообразования, значительный вклад в развитие которого внес В. Р. Волобуев, бросается в глаза, что рисунки с изображением почвенно-климатических ареалов и расчеты по энергетике почвообразования переходят из работы в работу без изменений в течение многих десятков лет (Волобуев, 1953, 1956, 1963, 1974; Глазовская, 1981; Добровольский, Урусевич, 2004). С одной стороны, это подтверждает фундаментальность полученных В. Р. Волобуевым результатов и перспективность поставленной им еще в 1945 г. задачи (Волобуев, 1945). Но, с другой стороны, на уровне теоретического понимания физической природы изучаемой взаимосвязи и выражения этого понимания в адекватных математических понятиях, демонстрируется явное отсутствие прогресса. В результате много десятилетий остается нерешенной интересная задача, которая потенциально могла быть решена еще в 50-60 гг. ХХ века.
В философско-методологических работах неоднократно рассматривался вопрос о том, что концептуальная революция в естествознании оказывается плодотворной только в том случае, если она дополняется конкретным математическим аппаратом, с помощью которого можно сформулировать основные, наиболее глубокие закономерности новой области действительности. Верно и обратное: математические методы могут оказать значительное воздействие на естествознание, только если им будет придан операционный смысл, если их признают описывающими реальные свойства природы, а не только формальные связи между ними (Акчурин, 1974, Овчинников, 1988). Иными словами, при изучении сложных иерархических систем, таких как почва, одновременная физико-теоретическая постановка задачи необходима не в меньшей степени, чем экспериментальные исследование. Перечислим некоторые характерные ошибки в работах, пренебрегающих анализом возможности построения адекватной математической модели, рассматриваемой задачи.
Почвоведение в значительной степени продолжает оставаться эмпирической наукой с соответствующими традициями простого перечисления использованных переменных, без включения их сразу в определенную теоретическую модель, соответствующую общей схеме решаемой задачи. Но за любым действием − измерением, определением понятия и др. − пусть и неявно, но всегда стоят какие-то допущения, определенные условия. Не учет этого обстоятельства, в конце концов может привести не только к понижению теоретического статуса полученного результата, но и кажущейся видимости решения поставленной задачи. Выбор произвольного числа переменных может означать, в частности, принятие методологии и картины мира классической физики, т.е. признание того допущения, что различные переменные не оказывают влияния на измерения величины других переменных. Сразу можно сказать, что для почв это является грубым приближением. Для них более адекватной является релятивистская или даже квантовая картина мира, учитывающие взаимовлияние между всеми почвенными свойствами, которыми принципиально нельзя пренебречь (Дышлевый, 1976). Последнее не означает необходимость применения математического аппарата теории относительности или квантовой механики в почвоведении. Речь идет о конкретной реализации принципа "генетической вековечной и всегда закономерной связи", категорически провозглашенного В.В. Докучаевым.
Ограничивая исследование установлением формальных корреляций между произвольными переменными, мы сразу отсекаем учет наиболее интересных нелинейных эффектов тонких взаимодействий между изучаемыми процессами, которые, как сейчас установлено, могут управлять глобальным поведением сложных систем, кардинально и резко меняя динамику и направление своего развития (Заславский, Сагдеев, 1988; Гапонов-Грехов, Рабинович, 1984; Ахромеева и др. 1992; Николис, Пригожин, 1990; Неймарк, Ланда, 1987). Формальное применение некоторых других статистических методов (главных компонент, факторный анализ и др.) зачастую также не позволяет изучать нелинейные эффекты, поскольку теоретическую основу этих методов составляют линейные модели.
При построении теоретической модели всегда следует думать о физической полноте набора независимых параметров и переменных, описывающих природное явление. Хотя основным в этом случае является глубокое качественное понимание изучаемого явления, существуют и формальные методы контроля. С этой целью используется анализ размерности, который, однако, тоже не полностью гарантирует от неправильной постановки задачи. В истории известны случаи, когда даже известные ученые получали формально верный, но физически ошибочный результат (Бриджмен, 2001). Отсутствие математической модели (схемы), как и нечеткое понимание задачи ведет к тому, что часто рассматриваются как системные любые работы лишь постольку, поскольку в них изучается некоторый произвольный набор переменных. Выбор уровня исследования зависит от поставленной цели, но раз он сделан, то предметная область должна быть определена таким образом, чтобы она представляла собой объективную целостность. Здесь выбор переменных ограничен.
Своеобразие системного подхода состоит в целостном видении объекта исследования. Изучение не полностью контролируемого объекта исследования, т. е. в котором признак целостности отсутствует, сразу же порождает теоретические и практические трудности. Например, встречаются режимные работы по изучению эрозии почв при снеготаянии (Танасиенко и др., 2013), продолжающиеся десятилетиями, методический смысл которых должен состоять в точных балансовых расчетах, но которые, даже без приблизительной оценки возникающей погрешности, пренебрегают очевидными приходно-расходными статьями. Понятно, что такие исследования оказываются малоэффективными. Оправданием низкой величины коэффициента корреляции ~ 0,5 в результирующем уравнении, связывающем осадки и сток, служит "универсальное объяснение" сложности учета всех обстоятельств.
Отмечается также несоблюдение норм системной методологии и в экологии почв, а именно с анализ климатических закономерностей без соблюдения требований обязательной выравненности всех остальных факторов (Соколов, 2004).
Построение и использование теоретической модели на любом этапе исследования автоматически повышает стандарты получения знания, обеспечивая таким работам по сравнению с эмпирическими большую правдоподобность и надежность. Это происходит хотя бы потому, что заставляет критически оценивать применяемые теоретические и экспериментальные методы.
В качестве последнего замечания, связанного с критическими анализом применения системного "экофизиологического", а по нашей терминологии, микроскопического подхода в почвоведении, сошлемся на статью заведующего лабораторией математического моделирования агроэкосистем Агрофизического Инстиута д.т.н. А. Г. Топаж с примечательным названием "Динамические модели продуктивности: тупик или распутье?". В ней приводится ссылка на мнение одного из создателей направления динамического моделирования в бывшем СССР О. Д. Сиротенко, высказаное в частном разговоре, что "время показало ограниченность и, в определенной мере тупиковость подхода, связанного с разработкой подобных моделей. ... Реальные практически задачи прекрасно решаются с привлечением простых методик регрессивного характера". Характеристики типа "овчинка оказалась совершенно не стоящей выделки", "шарлатанство", "кризис" и "возвращение к "примитивным" статистическим регрессионным моделям" и другие подобные выражения не раз встречаются в этой статье. В ней очень ярко и, с нашей точки зрения, совершенно точно отражена общая тенденция разочарования или, точнее, несоответствия полученных результатов завышенным ожиданиям не только по отношению к моделированию в сельском хозяйстве, но и к имитационному моделированию вообще.
Мы считаем, что "тупиковость" микроскопического подхода в имитационном моделировании продуктивности, так ярко охарактеризованная О.Д. Сиротенко, помимо объективной сложности объекта исследования, может быть связана с тем, что на пути от микроскопической постановки задачи (факторы и внутрипочвенные процессы) к получению макроскопического результата (продуктивность) был пропущен еще один важный иерархический уровень, на котором действуют свои закономерности, не сводящиеся к микроскопическим. Никакая вычислительная мощь компьютеров здесь не поможет. Необходимо найти качественно новые переменные, которые помогут сформулировать качественно новые закономерности. В нашем предположении мы опираемся на аналогию с развитием различных физических направлений. Дело выглядит так, как было в свое время с формулировкой законов статистической механики: движение каждой микрочастицы описывается законами Ньютона, но описать движение огромного числа частиц на их основе принципиально не представляется возможным. Решение нашел Дж.К. Максвелл, который понял, что прямолинейного микроскопического пути решения этой задачи не существует, нужна другая постановка вопроса: нужно ввести в физическую теорию представление о закономерностях особого типа, в которых связи между величинами, входящими в теорию, носят вероятностный характер. Так может оказаться и в случае с имитационным моделированием продукционного процесса − необходимо сначала догадаться о каких-то новых, промежуточных закономерностях внутрипочвенных явлений, сформулировать их и только потом выйти на задачу поиска связи этих закономерностей с продуктивностью агроценозов.
Сошлемся на подходящее к описываемой ситуации мнение одного из величайших физиков-теоретиков ХХ века Р. Фейнмана (1987): "Каждый раз, когда образуется длительный затор, когда накапливается слишком много нерешенных задач, это происходит потому, что мы пользуемся теми же методами, которыми пользовались раньше. Новую же схему, новое открытие нужно искать совсем на другом пути".
Таким образом , проведенный краткий критический анализ в отношении существующих подходов в почвоведении подтверждает нашу точку зрения о том, что в настоящее время актуальным является разработка именно мезоскопических моделей, избегающих крайностей как микроскопических моделей, стремящихся описать все и сразу, так и "простых и быстрых" макроскопических моделей, опирающихся на чрезмерно идеализированные представления о почвах. Проводя дальнейшую аналогию с физикой, можно сказать, что физика элементарных частиц и космология безусловно фундаментальные науки, но в нашем мире не все закономерности подчиняются их законам или сводятся к ним. Даже в рамках квантовой механики разрабатываются не только чисто квантовые методы. Свое право на существование и принципиальные преимущества доказали мезоскопические теоретические подходы, носящие названия полуклассических или квазиклассических приближений (Ландау, Лифшиц, 1989).
Постановка задачи
В настоящей работе на примере изучения взаимосвязей почв и атмосферного климата как фактора почвообразования представлены физико-теоретические основы нового мезоскопического подхода, который в определенном смысле рассматривает свойства и закономерности почв на масштабах, промежуточных между макроскопическим и микроскопическим. Его основу составляет традиционное представление о том, что структура почвенно-биоклиматических ареалов определяется одновременно как внешними факторами, так и внутрипочвенными процессами. Новизна заключается в методе расчета параметров совместного внутрипочвенного тепло-влагообмена (точнее − среднемноголетнего тепло-влажностного состояния почвенно-биоклиматических ареалов).
До описания математического содержания метода целесообразно кратко напомнить особенности макро-, микроскопического подходов и затем на качественном уровне детально описать физический смысл всех математических операций, совершаемых при разработке мезоскопического подхода.
Макроскопический уровень для нашей задачи задается внешними климатическими условиями: радиационным балансом R, осадками P, а также границами почвенно- биоклиматических ареалов как целостных единиц. Детализация внутренней структуры почвы, такая как профильное распределение гидро- и теплофизических коэффициентов, отсутствует. Почва представляется максимально идеализированным объектом − бесконечно тонкой пленкой. Из параметров R и P составляются комбинации (1) и (2), называемые гидротермическими коэффициентами, с которыми, по версиям М.И. Будыко (1956) и В.Р. Волобуева (1974), должны коррелировать границы почвенно-климатических ареалов (рис.1). Например, коэффициент увлажнения (1) соответствует определенным В.Р. Волобуевым гидрорядам. На рис.1 представлена структура почвенно-климатических ареалов, составленная на основе данных В.Р Волобуева (1974). Этот рисунок мы приводили ранее (Чичулин, 2019), и здесь воспроизводим его без изменения, как представляющий из себя важную часть базы эмпирических данных, используемой в дальнейших расчетах.
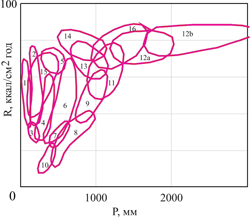
Рисунок 1. Расположение почвенно-климатических общностей по В.Р.Волобуеву (1974): 1 – пески пустынь, 2 – сероземы, 3 – бурые почвы полупустынь, 4 – каштановые почвы, 5 – каштановые почвы Африки, 6 – черноземы, 7 – серые лесные почвы, 8 – подзолы и подзолистые почвы, 9 – бурые лесные почвы, 10 – почвы тундр, 11 – желтоземы, 12 − красноземы и латериты (12а – основной ареал, 12b – более редкое распространение), 13 − коричневые почвы сухих лесов и кустарников (Африка), 14 – черные почвы саванн и тропических прерий, 15 – светло-бурые почвы тропических полупустынь, 16 – красно-бурые почвы саванн.
Микроскопический подход задается параметрами, характеризующими свойства почвенных горизонтов, отвечающих за внутрипочвенный тепло-влагообмен: гидро- и теплофизическими, а также перекрестными коэффициентами, динамикой внешнего климата R(t) и P(t) как граничными условиями, необходимыми для расчета динамики почвенного климата, а также границами почвенно-биоклиматических ареалов, как целостных единиц. Кроме границ почвенно-биоклиматических ареалов, остальные перечисленные коэффициенты в настоящей работе не использованы. По предположению, некоторые расчетные интегральные параметры почвенного климата (такие, как сумма температур выше 10 ˚С) должны коррелировать с определенными почвенно-климатическими ареалами.
Мезоскопический подход задается внешними климатическими характеристиками R и P, эмпирической функцией суммарного испарения почвенной влаги (испарение с поверхности почвы плюс транспирация) E(R, P) (3) и, как и в предыдущих двух случаях, границами почвенно-биоклиматических ареалов (рис.1). Деление почвы на горизонты отсутствует, и внутрипочвенный тепло-влагообмен рассматривается как целостный самоорганизованный процесс, согласованный с потоками обмена с внешней средой. Цель − найти интегральные характеристики этого самоорганизованного процесса для каждого почвенного ареала, которые и будут выражать искомую связь почв с климатическими условиями.
Поскольку целью настоящей работы является разработка именно мезоскопического подхода, опишем его по возможности подробнее. Его формальную основу составляют два взаимосвязанных постулата (принципа), которые можно назвать принципами инвариантности и оптимальности.
Принцип инвариантности
Постулат 1. Вся информация о структуре почвенно-биоклиматических ареалов в интегральной форме содержится в функции, определяющей величину суммарного испарения почвенной влаги в зависимости от средних многолетних значений радиационного баланса R и осадков P во всем диапазоне их изменения:
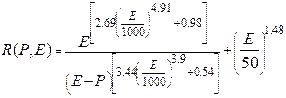
(3)
График изолиний функции испарения (3) приведен на рис. 2.
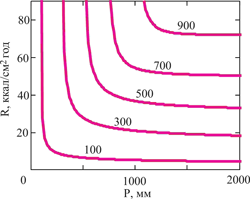
Рисунок 2. Изолинии испарения почвенной влаги, рассчитанные на основе уравнения (3), аппроксимирующего эмпирические данные, собранные В. Р. Волобуевым (1974). Цифры у изолиний обозначают величину функции суммарного испарения Е(R, P) в мм. Размерности величин такие же как на (рис.1).
Математически задача заключается в том, чтобы извлечь из функции испарения (3) информацию о структуре почвенно-биоклиматических ареалов (рис.1). С этой целью прежде всего необходимо записать функцию (3) в инвариантной форме. Способ, позволяющий это сделать, и составляет содержание принципа инвариантности. Поясним его.
Эмпирическое уравнение (3) мы вывели, используя базу данных, собранную В. Р. Волобуевым (1974). Подчеркнем, что величина суммарного испарения не измерялась, а рассчитывалась им как разница между суммарными многолетними осадками и стоком. Упоминание необходимости учета всего диапазона изменения радиационного баланса R и осадков P в этом уравнении является важным и сделано специально, чтобы подчеркнуть суть отличия мезоскопического подхода, в котором для расчетов используется вся функция испарения, от подходов М. И. Будыко (1956) и В. Р. Волобуева (1974), в гидротермических коэффициентах (1) и (2) которых используются только предельные значения этой функции, а именно испарение с поверхности предельно увлажненной почвы (по сути дела с поверхности свободной влаги) или полное испарение осадков (предельно сухое состояние почвы) (Чичулин, 2019).
Таким образом, в подходах М. И. Будыко (1956) и В.Р. Волобуева (1974) постулирована корреляция границ почвенно-климатических ареалов с независимыми макроскопическими коэффициентами (1) и (2). Отличие границ одних ареалов от других маркируется простыми множителями в этих коэффициентах − т. е. сводится к простому подобию.
В мезоскопическом же подходе утверждается, что диапазоны радиационного баланса и осадков, соответствующие различным почвенно-биоклиматическим ареалам, нельзя связать друг с другом простым умножением на некое число − коэффициент подобия. Связь между ними является более сложной. Кратко и с определенной долей условности можно сказать, что эта связь определяется одновременно двумя переменными коэффициентами подобия, которые вместе представляют собой одну функцию, имеющую два асимптотических предела.
С целью записи (3) в инвариантной форме из его составных частей конструируют новые переменные X и Y (4), такие, чтобы все изолинии суммарного испарения, изображенные на рисунке 1, сливались в одну универсальную зависимость. Способ конструирования новых переменных должен быть понятен из сравнения (3) и (4). По существу, он сводится к тождественной перестановке сомножителей в (3). Но, выраженная в новых переменных, функция испарения (3) приобретает новое качество: она представляет из себя гиперболическую зависимость, которая в двойных логарифмических координатах является прямой линией (5) (рис.3; А):
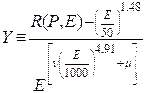
(4)
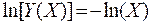
(5)
Смысл описанной операции заключается в том, что слияние в одну линию всех изолиний испарения означает, что будучи выраженными в новых переменных (4), все точки любых объектов, изображенных на экологическом поле (R, P), включая границы почвенно-климатических ареалов (рис.1) спроецируются на эту же линию (рис. 3; В). Таким образом, поиск аналитической зависимости структуры ареалов от климатических факторов, сведется к анализу их расположения на прямолинейной зависимости (рис.3; В, С).
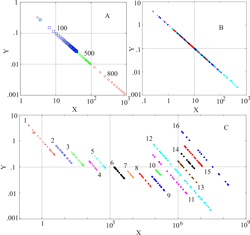
Рисунок 3. Почвенно-биоклиматические ареалы в обобщенных координатах. А − три изолинии суммарного испарения почвенной влаги в новых обобщенных координатах Y, X при Е1=100 мм/год (синие крупные квадраты), Е2=500 мм/год (зеленые средние треугольники), Е=800 мм/год (красные маленькие кружочки). Обобщенные координаты Y, X определены в тексте. В − границы всех почвенно-биоклиматические ареалы в новых координатах − спроецированы на одну линию. С − те же ареалы, с целью оценить относительные размеры каждого, сдвинуты друг относительно друга на постоянный шаг по оси Х. Цифры обозначают номера ареалов, соответствующие номерам на рисунке 1. Ареалы представляют из себя прямолинейные отрезки, отличающие друг от друга средней метрикой (масштабом).
Дадим теперь формальное определение: принцип инвариантности заключается в нахождении преобразований, оставляющих уравнение (3) в инвариантной форме.
Методологический смысл поиска инвариантной формы уравнений более глубокий, чем просто формальный прием. Инвариантность является фундаментальным принципом современной теоретической физики. Его эвристическое значение заключается в том, что он позволяет находить новые законы природы. Поскольку это очень важный вопрос, сделаем отступление и рассмотрим его подробнее.
Методологическое значение принципа инвариантности
Научные направления, обладающие относительно слабо развитым арсеналом собственных теоретико-познавательных средств, с целью повышения уровня теоретических исследований часто привлекают конкретные методы, разработанные на основе фундаментальных методологических принципов. При решении специальных задач эти методы могут модифицироваться, а используемые в них понятия приобретать новый смысл и значения.
Среди методологических принципов, использованных при разработке теоретических основ мезоскопического подхода − математизации, инвариантности, целостности, иерархичности, относительности, локальности, соответствия и дополнительности − не все играют одинаковую роль. Большинство из них даже не упоминается. Но принцип симметрии мы выделяем как центральный (Овчинников, 1988; 1996; 2009). Отчасти в этом сказываются собственные интересы автора, однако основная причина заключается в том, что различные виды симметрии и связанные с ними законы сохранения объективно отражают наиболее фундаментальные структурные свойства действительности (Любарский, 1986; Урманцев, 1974). Подтверждением служит то, что в настоящее время в самых различных научных направлениях, и, безусловно, прежде всего в физике, принципы симметрии, в форме конкретных законов сохранения, закона инерции Гилилея в механике, уравнений Максвелла в электродинамике, первого начала термодинамики и др., составляют аксиоматическую основу соответствующих теорий. К тому же принципы симметрии, в отличие от других, обладают собственным математическим аппаратом − теорией групп, предназначенной для извлечения следствий из свойств симметрии изучаемых объектов. Многие полагают, что в математическом аппарате современной физики теоретико-групповые структуры заняли сегодня ведущее место, оттеснив на второй план дифференциально-аналитические структуры, присущие классической физике (Разумовский, 1986).
Эвристические функции принципов симметрии состоят в том, что они дают возможность получать количественную информацию о сложных природных системах даже в тех случаях, когда уравнения, описывающие эти системы, неизвестны (Любарский, 1986;. Преображенский, 1986.). Эти свойства принципов симметрии утвердили их в роли мощного методологического и теоретического средства при решении многих, а не только физических проблем.
Существуют различные виды симметрии − зеркальная, трансляционная, вращательная и др. Их общий смысл понятен из названия. Калибровочная симметрия, которая применяется в настоящей статье − одна из разновидностей симметрии, связанная с инвариантностью уравнений, относительно масштабных преобразований фигурирующих в них переменных.
В определенном смысле математическая теория групп, среди прочих методов, занимает место на границе между качественными и количественными подходами. Преимущество такого положения в том, что нет необходимости разрабатывать сложный математический аппарат, его можно "угадать". Однако "угадать" − не значит "легко". Сделать это можно только на основе глубокого понимания сути изучаемого явления на качественном уровне. Необходимым условием при этом оказывается рассмотрение многочисленных и взаимосвязанных проблем эмпирического, предметно-теоретического и системно-методологического уровней описания.
Мотивацией проявления интереса к применению симметрии в нашей работе явилось то, что, во-первых, в настоящее время принципы симметрии доказали свою высочайшую эффективность в теоретической физике. Теория групп занимает сегодня одно из ведущих мест в ее математическом аппарате. Даже эмоциональная характеристика первоначального взрывного интереса к применению симметрийного анализа в физике ХХ века как "теоретико-групповой чумы", в известной степени свидетельствовала об эффективности и эвристических возможностях применения теории групп к различным задачам. Вряд ли такое название было бы дано при полном отсутствии результативности. Можно сказать, что в настоящее время утвердилась особая роль принципов симметрии при построении физической теории. Теоретико-инвариантный подход проник в физику и определил целесообразность формулирования физических теорий именно на основе принципов симметрии. Во-вторых, некоторые задачи, стоящие перед генетическим почвоведением, напрямую перекликаются с задачами, в решении которых теоретико-групповые методы достигли наиболее заметных результатов. Мы имеем в виду группировки различных структурных единиц природы. Перечислим их.
1. Классическим примером является классификация всех возможных дискретных кристаллических форм, проведенная в 1890 г. в работах Е. С. Федорова и А. Шенфлиса (Разумовский О. С. 1979; Бир, Пикус, 1972). Это был первый в истории случай применения теории групп в естествознании, приведший к появлению теоретической кристаллографии.
2. Впечатляющим оказалось применение теории групп в физике элементарных частиц, которых на сегодняшний день насчитывается более 700 (вместе с античастицами). Теория групп позволила построить эвристически эффективную схему их классификации, лежащую в основе Стандартной модели, объединяющей сильные, слабые и электромагнитные взаимодействия.
3. Большой интерес представляют попытки применения теории групп для классификации химических элементов. Известно, что таблица Менделеева построена на обобщении феноменологических свойств элементов. Однако, было показано (Румер, Фет, 1971; Конопельченко, Румер, 1979) что возможен и другой путь классификации - постулировать группу симметрии и, исходя из нее, сгруппировать элементы. При этом выяснились интересные подробности, связанные, в частности, с обнаружением большого количества пустых клеток, которые пытаются идентифицировать, хотя и с большой осторожностью (Кулаков, 1991; Кулаков, 2004).
4. В настоящее время на основе принципа калибровочной симметрии строится единая теория всех четырех фундаментальных взаимодействий в физике. Физики считают, что дискредитированный в свое время термин "единая теория поля" приобретает в теории калибровочных полей новое, вполне реальное звучание. (Преображенский, 1979; Девис, 1989).<
Это лишь малая часть наиболее заметных достижений, связанных с применением теории групп. Перечислить все просто невозможно. Но ясно, что принцип симметрии, уже сегодня прочно вошел в арсенал теоретической физики.
Таким образом, применив принцип инвариантности, мы получили в качестве промежуточного результата прямолинейные зависимости, изображенные на (рис.3; В, С). Напомним, что эти прямые являются изображениями границ почвенно-биоклиматических ареалов. Далее необходимо для каждого ареала рассчитать интегральные параметры внутрипочвенного климата. Трудность заключается в том, что напрямую рассчитать их из промежуточных результатов (рис.3; В, С) нельзя. Дело в том, что, хотя отрезки, характеризующие почвенно-биоклиматические ареалы, лежат на одной прямой, их внутренние масштабы различны. Строго говоря, каждая точка экологического поля (R, P), пересчитанная в новых координатах, обладает своим масштабом, определяемым функцией испарения, поэтому уравнение (5) неоднородно. В каждой его точке свой масштаб, который зависит от величины испарения по правилам, определяемым новыми переменными (4). Эта особенность уравнения (5) делает неприменимыми к нему стандартные математические методы анализа однородных прямых. Новый же метод расчета еще необходимо поискать. Содержание этого метода и определяется вторым постулатом мезоскопического подхода − принципом оптимальности.
Принцип оптимальности
Для этого вернемся несколько назад и обратим внимание на то, что в определениях новых переменных (4) есть параметры μ и ν, варьирование которых симметричным образом не изменяет уравнение (5). Выражение "симметричным образом" означает, что когда эти параметры в одной переменной X уменьшается на определенную величину, то на такую же величину во второй переменной Y они увеличивается и наоборот. При варьировании происходит смещение точек, изображающих почвенно-биоклиматические ареалы, вдоль прямой (5), изменяются расстояния между ними, но само уравнение (5) графически остается неизменным. Чтобы отчасти пояснить ситуацию, на (рис.4 А), в качестве типичного примера, изображены смещения максимальной и минимальной границы черноземного ареала (№ 6) при варьировании параметра ν. Варьирование параметра μ вносит малый вклад и поэтому вместо него принято постоянное среднее значение μ = 0.98. Для определенности, параметр ν далее будем называть масштабным фактором
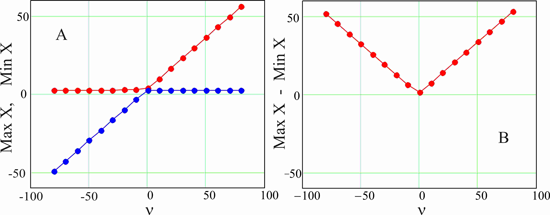
Рисунок 4. Смещение максимальных (красные точки) и минимальных значений (синие точки) обобщенной переменной Х для границ черноземного ареала при изменении параметра ν. Смещение переменной Y происходит таким же образом, но с противоположным знаком. (А) −смещение значений по отдельности. (В) − смещение разности максимального и минимального значения. Рисунок изображает поведение смещений в мелком масштабе для того, чтобы был ясен общий ход зависимости. Точные значения параметра (масштабного фактора) ν, при котором функция достигает минимума для черноземного ареала ν = − 0.89. Характерные точки перегиба отделяют преобладающий сдвиг всех точек ареалов по разным ветвям переменных Х или Y. Вблизи точки минимума (рис.4В) точки ареала максимально сближаются друг с другом, размеры ареала становятся минимальными, так, что длина каждой линии, обозначающей соответствующий ареал на (рис.3 С) тоже становится минимальной. Каждый ареал характеризуется своим значением ν, при котором достигается минимум.
Опишем результаты математических расчетов изменения структуры ареалов при изменении масштабного фактора ν. Все точки, изображенные на рис.4, удовлетворяют уравнению (5). На этом этапе задача заключается в том, чтобы избавиться от этой неоднозначности и найти какие-то уникальные значения новых переменных, для того, чтобы уравнение (3) обладало не только формальной инвариантностью, но и физическим смыслом. На рис. 4 видно, что на кривых существуют характерные точки перегиба. Такие перегибы существуют для каждой точки нового экологического поля (Х, Y). (Новым мы назвали его для того, чтобы отличать от старого экологического поля (R, P)). Точки перегиба отделяют смещения точек ареалов по разным ветвям новых переменных. При изменении масштабного фактора ν все точки, расположенные на новом экологическом поле (X, Y), изменяют свое месторасположение. Но все они при изменении масштабного фактора ν движутся с разной скоростью либо в направлении, определяемом переменной Х (вдоль ветви Х), либо в направлении, определяемом переменной Y (вдоль ветви Y). И только при определенном значении параметра ν, точки ареалов группируются максимально плотно, когда переходят с одной ветви на другую.
Далее, движение точек ареалов происходит таким образом, что когда одна точка ареала (max) движется по одной ветви, вторая точка ареала (min) практически стоит на месте. При достижении параметром ν точки перегиба движение точек ареалов изменяются: первая точка замедляет движение и практически останавливается, а вторая начинает двигаться по другой ветви. Таким образом, физический смысл параметра ν заключается в том, что он характеризует перераспределение масштабов между новыми переменными X и Y (4). Напомним, что переменная Y связана с радиационным балансом и испарением, а переменная Х − с осадками и испарением. Поэтому Y можно рассматривать как нормированный радиационный баланс, а Х − как нормированные осадки. При перераспределении масштабов (нормировок) есть выделенная ситуация, когда размеры ареала принимают единственное минимальное значение (рис.4 В). Интерпретировать эту ситуацию можно как достижение оптимального соотношения между теплом и влагой в почве, соответствующее заданным внешним факторам R и P. Величины масштабных факторов ν, рассчитанные для каждого почвенно-биоклиматического ареала приведены на рис. 5. Интересно отметить, что почвы, сформированные в предельно сухих и предельно холодных климатических условиях, характеризуются низкими значениями масштабного фактора, тогда как остальные − значениями ν, близкими друг к другу и к нулю.
Полученный результат можно сформулировать в виде второго основного постулата (принципа оптимальности) мезоскопического подхода:
Постулат 2. Из всех возможных вариантов перераспределения тепла и влаги внутри почвы при заданных внешних факторах R и P, реализуется тот, при котором размеры заданного почвенно-биоклиматического ареала, выраженные в обобщенных переменных (X, Y), являются минимальными.
Таким образом, применив последовательно принципы инвариантности и оптимальности, мы решили задачу, а именно нашли преобразования, оставляющие функцию испарения (3) инвариантной при изменении внешних факторов R и P. Для этого к гидротермическим параметрам каждого ареала пришлось применить локальные калибровочные преобразования, связывающие старые переменные R и P с новыми переменными X и Y (4). Отметим, что в физике прямым аналогом для этих преобразований являются преобразования Лоренца в специальной теории относительности, связывающие между собой пространственные и временные координаты в различных инерциальных системах отсчета, движущихся с некоторой скоростью друг относительно друга. В мезоскопическом подходе аналогом этой скорости являются изолинии испарения. Вывод, который вытекает из полученных результатов, по своей сути согласуется с выводом специальной теории относительности: нельзя напрямую сравнивать почвы, сформированные при различных климатических условиях, они несопоставимы. Для корректного сравнения этих условий, их необходимо сначала подвергнуть преобразованиям (4).
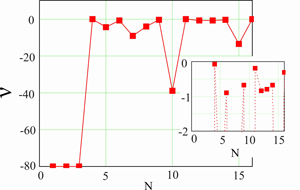
Рисунок 5. Величины масштабных факторов ν для всех почвенно-биоклиматических ареалов. N − номера ареалов, соответствующие (рис.1). На врезке справа изображена верхняя часть основного графика в увеличенном масштабе.
В процессе построения мезоскопического подхода исключительно теоретическим путем найдена новая, специфическая для каждого почвенного ареала, величина − масштабный фактор ν. Физический смысл этого фактора − служить количественной характеристикой оптимального соотношения между внутрипочвенными величинами тепла и влаги. С его помощью рассчитываются интегральные внутрипочвенные гидротермические характеристики (4) через внешние факторы R и P и функцию испарения Е(R, P) (3). Но физический смысл этого фактора шире, и выходит за пределы параметров, определенных по условию задачи: R, P, E(R, P). По существу, масштабный фактор говорит о том, что этих параметров недостаточно для полной характеристики почвы. Механизмы, с помощью которых почва может влиять на установление оптимального соотношения тепла и влаги − это перестройка структуры, состава и свойств существующих и появление новых почвенных горизонтов, изменение количества и качества растительности и т. п. Масштабный фактор интегральным образом связан именно с этими механизмами. Дальнейшее развитие теории мезоскопического подхода и установление его связей с экспериментальными исследованиями может идти и в этом направлении.
В качестве конкретного примера применения масштабного фактора совместно с другими параметрами на рис. 6 приведена группировка почвенно-климатических ареалов, полученная в рамках мезоскопического подхода. Подчеркнем, эта группировка получена исключительно расчетным методом, без привлечения качественных соображений о том, где какой ареал должен располагаться. В этом состоит одно из отличий результатов работы В. Р. Волобуева и нашей.
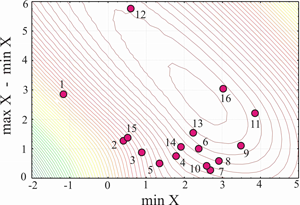
Рисунок 6. Расположение параметров почвенно-биоклиматических ареалов на изолиниях масштабного фактора ν.
Рисунок 6 следует сравнивать с рис.1 настоящей работы или с рис. 33 работы В.Р. Волобуева (1974). Работа в этом направлении еще не окончена, поэтому окончательных выводов мы пока не делаем, но хотим обратить внимание на закономерную и ступенчатую организацию в расположении ареалов. Кроме того, наблюдается тесная (полная и не могла быть) корреляция в расположении гидро- и терморядов В. Р. Волобуева и изолиний масштабного фактора ν.
Методологическое значение принципа оптимальности
Возвращаясь к принципу оптимальности следует отметить, что, судя по всему, его можно интерпретировать как конкретную реализацию всеобщего принципа оптимального устройства природных объектов − многократно подтвержденной общей природной закономерности (Розен, 1969; Ассеев, 1977). В физике такие принципы носят название экстремальных или вариационных.
По поводу экстремальных принципов целесообразно сделать несколько замечаний. Представление о том, что природа во всех своих проявлениях стремится к экономии, является одним из старейших принципов теоретической науки. Физика дает ряд превосходных примеров задач такого рода. Один из первых примеров − основной принцип геометрической оптики − принцип наименьшего времени Ферма. Аналогом принципа Ферма в механике является известный принцип наименьшего действия Мопертюи (Ассеев, 1977.) Дальнейшее развитие экстремальных принципов привело к осознанию их огромной теоретической значимости и общности. Например, на принципе минимального действия Гамильтона построена большая часть всемирно известного курса теоретической физики Л.Д. Ландау, И.М. Лифшица. Из этого принципа выводятся законы Ньютона, Максвелла, Шредингера, Эйнштейна.
В физике возможность построить альтернативные теории для одной и той же предметной области на разных основаниях осознана давно − со времен создания механики Лагранжа и Гамильтоновой. В математике − со времен создания неевклидовых геометрий. Построение физических теорий на основе экстремальных принципов относится к таким альтернативным теориям. В мезоскопическом подходе, описанном в настоящей работе, насколько нам известно, впервые применен экстремальный принцип при решении задачи о зависимости почв от климатических условий. Показано, что альтернативность не означает тождественность. Мезоскопический подход обладает определенными преимуществами и перед микроскопическим и перед макроскопическим подходами. Концентрированное сравнение этих подходов между собой изображено на рис. 7.
Важно подчеркнуть, что каждая из альтернативных формулировок обладает своими преимуществами перед другими. В мезоскопическом подходе таким преимуществом является возможность расчета оптимального соотношения тепла и влаги в почве без знания ее внутренней структуры. Дальнейшее применение мезоскопического подхода достаточно очевидно и может быть связано с возможностью прогнозировать направление эволюции почв, вслед за изменяющимися климатическими условиями или проведением более детальной группировки почв, чем описанные в настоящей работе почвенно-биоклиматические ареалы, и многое другое.
Следует сказать, что с формальной точки зрения принцип оптимальности играет роль постулата, т.е. утверждения, лежащего в основе разрабатываемого теоретического подхода. Постулат логически не выводится из более фундаментальных законов, и в этом смысле его нельзя ни подтвердить, ни опровергнуть. Его правильность обосновывается эвристическими рассуждениями и здравым смыслом и проверяется в дальнейшем на достоверность сравнением с опытом вытекающих из теоретической модели следствий.
Обратим внимание на то, вместо решений дифференциальных уравнений с граничными условиями в мезоскопическом подходе используется другая информация − о зависимости суммарного испарения почвенной влаги от климатических характеристик. Эта функция в интегральной форме содержит информацию о специфике взаимодействия тепла и влаги в профиле почвы и растительности. Она является эмпирической основной для всех последующих расчетов. Поэтому, по аналогии с ОГХ − основной гидрофизической характеристикой, предложенной А. М. Глобусом (1983, 1987), для краткости ссылок и упоминаний, предлагается аббревиатура ОГТХП − основная гидротермическая характеристика почвообразования − поскольку из нее, при соответствующих допущениях, выводится вся остальная информация о почвах.
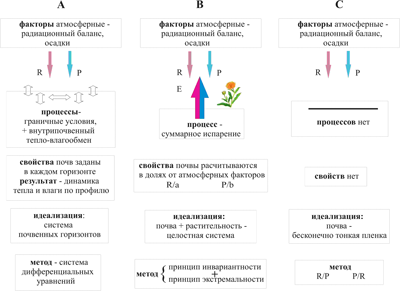
Рисунок 7. Схема, иллюстрирующая специфику микроскопического (А), мезоскопического (В) и макроскопического (С) подхода. Схема построена в соответствии с формулой: факторы → процессы → свойства, дополненной описанием принятой идеализации и основным методом расчета.
Заключительные замечания о принципах симметрии
Р. Фейнман в своей замечательной книге "Характер физических законов" (1987) назвал законы сохранения великими. Но известно, что законы сохранения являются следствием принципов симметрии. Значит ли это, что принципы симметрии являются еще более великими, в смысле - более общими? В определенном смысле да. Сошлемся на еще одного из виднейших физиков-теоретиков ХХ в. Е. Вигнера, который в лекции, посвященной вручению ему Нобелевской премии (1965) назвал принципы симметрии "законами законов". Выше, в параграфе, посвященном методологическому значению принципов инвариантности, была отмечена лишь малая часть огромных достижений, полученных с помощью этих принципов в науке. Но закономерен вопрос: почему же столь эффективное средство теоретического анализа как принципы инвариантности до сих пор пренебрежимо мало используется в почвоведении? Перефразируя того же Е. Вигнера (1968) можно использовать более энергичное выражение о "непостижимой неэффективности" математики в почвоведении. Вряд ли можно дать однозначный ответ, во всяком случае, такой, с которым согласится большинство почвоведов.
Некоторые объективные и субъективные причины этой "непостижимой неэффективности" мы постарались рассмотреть выше в параграфе, посвященном критическому рассмотрению применения системного подхода в почвоведении. Приведем еще некоторые примеры, поясняющие нашу позицию в этом вопросе, хотя отдаем себе отчет в том, что для многих они могут показаться неубедительными.
Если различать теоретический и эмпирический уровни исследования, то учение о почвах по применяемым методам исследования в настоящее время в целом продолжает оставаться эмпирической наукой. Понимание этого демонстрирует использование понятия "учение" вместо "теория", в названиях фундаментальных работ В.А. Ковды "Основы учения о почвах" или А.А.Роде "Основы учения о почвенной влаге". Использование понятия "учение" не означает уничижительного отношения. Существует же, например, "христианское учение". Просто учение − это не теория. Вместо понятия "учение" можно использовать понятие "общая теория".
Теоретические элементы, присутствующие в генетическом почвоведении, например − законы почвообразования, первые формулировки которых были даны еще В. В. Докучаевым, получены как индуктивные обобщения эмпирических данных и в большинстве своем до сих пор не перешли со стадии качественных утверждений на количественную.
И наконец, для развития специальной физико-теоретической дисциплины также недостаточно введения многочисленных образных и метафорических качественных понятий типа "почва-память", "почва-функция", "почва-отражение" или дискуссии о том, какой термин является более удачным − "почва-момент" или "почва-жизнь" (Соколов, 2004). Это свойственно скорее поэзии, а не науке. В каких-нибудь науках еще, кроме почвоведения, существует подобная система понятий? Более близкой нам представляется точка зрения Р. Фейнмана (1987) о том, что расплывчатая теория позволяет получать любые результаты, вплоть до противоположных. Или известная позиция выдающегося физика-теоретика, одного из создателей квантовой механики и общей теории поля В. Гейзенберга (1989), утверждавшего, что физическая теория не должна содержать лишних понятий, которым не соответствует непосредственно наблюдаемые величины. Нам представляется, что мезоскопический подход, описанный в настоящей работе, удовлетворяет строгим требованиям, предъявляемым к физико-теоретическим подходам.
Выводы
Цель работы заключалась в разработке физико-теоретических основ мезоскопического подхода к изучению количественных взаимосвязей "почва - климат". При этом за эмпирическую основу были взяты величины, которые нужно, а не те, которые можно легко измерить.
В техническом отношении мезоскопический подход разрабатывался путем постепенной трансформации макроскопического подхода:
замены испарения с поверхности свободной влаги на испарение из почвы и транспирацию. Вместо формул (1) и (2) по отдельности, используется обобщающая их формула (3);
разделения функции испарения (3) на две новые переменные (вместо старых - E, R, P) и интерпретация их как обобщенных переменных в смысле теории подобия. Запись инвариантного уравнения, связывающего новые обобщенные переменные;
варьированием масштаба в определениях обобщенных переменных находится условие инвариантности (устойчивости) границ почвенных ареалов. В форме (пока временной) гипотезы формулируется принцип оптимальности для соотношения тепла и влаги для каждого почвенного ареала и вводится масштабный фактор, как количественный показатель этого соотношения - ν.
Одна из задач мезоскопического подхода − определить параметры, характеризующие интегральное гидротермическое состояние почвы без информации о гидро-теплофизических свойствах почвенного профиля. Эта информация заменяется на знание функции суммарного испарения почвенной влаги. Показано, что новые переменные Х и Y (4), введенные с целью записи функции испарения (3) в инвариантной форме, решают эту задачу − устанавливают искомую связь внутрипочвенного гидротермического состояния от внешних климатических факторов R и P.
Одновременно с этим новые переменные X и Y интерпретированы как детализация введенного В.Р. Волобуевым коэффициента полноты использования радиационной энергии. В этом смысле новые переменные являются соответственно коэффициентами полноты использования тепла и влаги в почве.
Сформулирован новый принцип оптимальности, утверждающий, что почва приходит в равновесие с внешними факторами при определенном соотношении внутрипочвенных тепла и влаги. Следствием принципа оптимальности явилась необходимость введения нового параметра − масштабного фактора ν, количественно характеризующего это соотношение. Таким образом показано, что в задаче о почвенно-климатических взаимосвязях, должны существовать оптимальные соотношения не только между внешними и внутренними гидротермическими факторами в целом, но и между теплом и влагой внутри почвы.
Рассчитаны масштабные факторы ν для каждого почвенно-биоклиматического ареала. Показано, что они закономерно изменяются в зависимости от внешних климатических условий и могут служить индикатором эволюционных изменений почвенных свойств при изменении климата.
В перспективе принцип оптимальности и масштабный фактор могут служить рабочими инструментами для выделения однородных подсистем − ареалов в пределах заданных почвенных общностей. В этом заключаются дальнейшая возможность применения принципа оптимальности в почвоведении и установление связи масштабного фактора с экспериментально определяемыми свойства почв.
С использованием новых переменных и масштабного фактора получена новая группировка почвенно-биоклиматических ареалов, отличающаяся от группировки В. Р. Волобуева в существенных деталях. Ее отличительной особенностью (и преимуществом) является то, что она получена полностью теоретическим методом - расчетом из функции испарения.
Показано, что новые обобщенные переменные X и Y не противоречат традиционным гидротермическим коэффициентам (1) и (2), но асимптотически связаны с ними. В этом смысле новые переменные являются обобщением гидротермических коэффициентов и одновременно устанавливаю логическую (системную) связь между ними.
В почвенно-климатических закономерностях обнаружено несколько новых преобразований симметрии − при выводе универсального уравнения (4); при формулировке принципа оптимального перераспределения тепла и влаги в почве;
Преимущество масштабного фактора перед гидро- и терморядами В.Р. Волобуева заключается в том, что последние лишь в промежуточной асимптотике коррелируют с границами ареалов. В мезоскопическом подходе масштабный фактор совпадает с ними полностью.
Финансовая поддержка
Работа выполнена при финансовой поддержке Министерства высшего образования и науки Российской Федерации по государственному заданию Института почвоведения и агрохимия СО РАН, г. Новосибирск.
Литература
Абрамова Н.Т. Редукционистские тенденции кибернетики // Кибернетика и диалектика. М.: Наука, 1978. С. 287-306.
Агошкова Е.Б., Ахлибинский Б.В., Флейшман Б.С. Системология: сущность и место в научном знании // Синергетика и методы науки. С.-Петербург: Наука, 1998. С. 63-76.
Акчурин И.А. Единство естественно-научного знания. М.: Наука, 1974. 208 с.
Асеев В.А. Экстремальные принципы в естествознании и их философское содержание. Л.: Изд-во ЛГУ, 1977. 232 с.
Ахромеева Т.С., Курдюмов С.П., Малинецкий Г.Г., Самарский А.А. Нестационарные структуры и диффузионный хаос. М.: Наука, 1992. 544 с.
Бир Г.Л., Пикус Г.Е. Симметрия и деформационные эффекты в полупроводниках. М: Наука, 1972. 584 с.
Бриджмен П. Анализ размерности. Ижевск: НИЦ "Регулярная и хаотическая динамика", 2001. 148 с.
Будыко М.И. Тепловой баланс земной поверхности. Л.: Гидрометеоиздат, 1956. 256 с.
Вигнер Е. События, законы природы, принципы инвариантности // Успехи физических наук. 1965. Том 85. Вып. 4. С. 727-736.
Вигнер Е. Непостижимая эффективность математики в естественных науках // Успехи физических наук. 1968. Том 94. Вып. 3. С. 535-546.
Волобуев В.Р.Экология почв. Баку: Изд-во АН Азер. ССР, 1963.
Волобуев В.Р. Введение в энергетику почвообразования. М.: Наука, 1974. 128 с.
Волобуев В.Р. Климатические условия и почвы // Почвоведение. 1956. № 4. С. 24-37.
Волобуев В.Р. О почвенно-климатических ареалах // Почвоведение. 1945. № 1. С. 3–16.
Волобуев В.Р. Почвы и климат. Баку: Изд. Акад. наук Азерб. ССР., 1953. 320 с.
Волобуев В.Р. Система почв мира. Баку: ЭЛМ, 1973. 308 с.
Гапонов-Грехов А.В. Рабинович М.И. Нелинейная физика. Стохастичность и структуры // Физика ХХ века. Развитие и перспективы. М.: Наука, 1984. С. 219-280.
Гейзенберг В. Физика и философия. Часть и целое. М.: Наука, 1989. 400 с.
Гладышев Г.П. Термодинамика и макрокинетика природных иерархических процессов. М.: Наука, 1988. 287 с.
Глазовская М.А. Общее почвоведение и география почв. М. Высшая школа. 1981. 400 с.
Глобус А. М. Почвенно-гидрофизическое обеспечение агроэкологических математических моделей. Л.: Гидрометеоиздат, 1987. 427 с.
Глобус А. М. Физика неизотермического внутрипочвенного влагообмена. Л.: Гидрометеоиздат, 1983. 278 с.
Гухман А. А. Введение в теорию подобия. М.: "Высшая школа", 1973. 296 с.
Девис П. Суперсила. Поиски единой теории природы. М.: Мир, 1989. 272 с.
Добровольский Г.В. Философские аспекты генетического почвоведения // Почвоведение, 2004. № 8. C. 901-910.
Добровольский Г.В., Урусевская И. С. География почв. М. Изд-во МГУ. 2004. 460 с.
Дружининин Д. Л., Ванярхо В. Г. Синергетика и методология системных исследований // Системные исследования. М.: Наука, 1989. С. 283-303.
Дышлевый П.С. Эволюция "принципов описания" в физическом познании // Философские основания естественных наук. М.: Наука, 1976. С. 91-117.
Заславский Г. М., Сагдеев Р. З. Введение в нелинейную физику. От маятника до турбулентности и хаоса. М.: Наука, 1988. 368 с.
Конопельченко Б.Г., Румер Ю.Б. Атомы и адроны (Проблема классификации) // Успехи физических наук. 1979. Т.129. Вып.2. С.339-345.
Кулаков Ю. И. Классификация химических элементов на новой основе // Классическое естествознание и современная наука. Новосибирск: Изд-во НГУ, 1991. С. 97-118.
Кулаков Ю.И. Теория физических структур. Новосибирск: Изд-во "Альфа Виста", 2004. 851 с.
Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. Т.3. М.: Наука, 1989. С. 768.
Любарский Г.Я. Теория групп и физика. М.: Наука, 1986. 224 с.
Мичурин Б.Н. Энергетика почвенной влаги. Л.: Гидрометеоиздат, 1975. 141 с.
Неймарк Ю. И., Ланда П. С. Стохастические и хаотические колебания. М.: Наука, 1987. 424 с.
Николис Г., Пригожин И. Познание сложного. Введение. М.: Мир, 1990. 344 с.
Овчинников Н. Ф. Принципы сохранения. Законы сохранения. Симметрия. Структура. М.: Книжный дом "ЛИБРОКОМ", 2009. 336 с.
Овчинников Н.Ф. Принципы теоретизации знания. М.: Институт философии РАН, 1996. 215 с.
Овчинников Н.Ф. Тенденция к единству науки. М.: Наука, 1988. 272 с.
Онищенко В.Г. Подобие термодинамических характеристик почвенной влаги и их обобщенное описание. Автореферат дис. доктора сельскохозяйственных наук. М.: 1988. 48 с.
Пачепский Я.А. Математические модели физико-химических процессов в почвах. М.: Наука, 1990. 188 с.
Полуэктов Р.А., Смоляр Э.И., Терлеев В.В. Топаж А.Г. Модели продукционного процесса сельскохозяйственных культур. Изд-во С.-Петербургского ун-та, 2006. 396 с.
Преображенский Н.Г. Эвристический характер свойств симметрии в физике // Методологические проблемы математической физики. Новосибирск: Наука, Сиб. отд., 1986. с. 232-245.
Разумовский О.С. Теория групп // Методологические проблемы математической физики. Новосибирск: Наука, Сиб-е отде-е, 1986. с. 225-231.
Розен Р. Принцип оптимальности в биологии. М.: "Мир", 1969. 216 с.
Румер Ю.Б., Фет А. И. Группа Spin(4) и таблица Менделеева // Теор. и мат. физика. 1971. Т. 9. № 2. С.203-210.
Садовский В. Н. Основания общей теории систем. Логико-методологический анализ. М.: Наука, 1974. 280 с.
Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1981. 448 с.
Сиротенко О.Д. Математическое моделирование водно-теплового режима и продуктивности агроэкосистем. М.: Гидрометеоиздат, 1981. 166 с.
Соколов И.А. Теоретические проблемы генетического почвоведения. Новосибирск: "Гуманитарные технологии", 2004. 288 с.
Танасиенко А.А., Чумбаев А.С. Якутина О.П. Миллер Г.Ф. Условия и интенсивность эрозионно-аккумулятивных процессов Предсалаирья // Почвоведение. 2013. № 11. С.1397-1408.
Топаж А.Г. Динамические модели продуктивности: тупик или распутье? СПб.: АФИ, 2014. С. 48-69.
Урманцев Ю.А. Симметрия природы и природа симметрии. Философские и естественно-научные аспекты. М., 1974. 229 с.
Усков И.Б., Моисеев К.Г. Развитие моделирования с приложением теории и методов подобия в агрофизике // Агрофизика. 2018. №1. С. 53-63.
Фейнман Р. Характер физических законов. М.: Наука, 1987. 160 с.
Чичулин А.В. Методологический анализ понятийного аппарата в экологии почв // Почва и окружающая среда. Том 2. № 3. 2019. e89.
Сведения об авторе:
Чичулин Александр Валентинович – кандидат биологических наук, старший научный сотрудник лаборатории почвенно-физических процессов Института почвоведения и агрохимии СО РАН (Новосибирск, Россия); chichulin@issa-siberia.ru
Автор прочитал и одобрил окончательный вариант рукописи
 Статья доступна по лицензии Creative Commons Attribution 4.0 License
Статья доступна по лицензии Creative Commons Attribution 4.0 License
PHYSICO-THEORETICAL BASIS OF THE MESOSCOPIC APPROACH TO STUDY SOIL-CLIMATIC REGULARITIES
A.V. Chichulin 
Address: Institute of Soil Science and Agrochemistry of Siberian Branch of the Russian Academy of Sciences, Novosibirsk, Russia
Aim of the study. The aim of the work was to review critically the practice of applying system approach in soil research and identify existing problems; to consider the cognitive potential of micro- and macroscopic approaches in computational simulation of soil-bioclimatic regularities.
Methodology. Mathematical simulation.
Results of the study. A new mesoscopic approach to the study of the structure of soil-bioclimatic areas is proposed. It is based on two principles referred to as the principle of invariance and the principle of optimality. Application of these principles makes it possible to express the regularities in soil-climate relationship in the form of a single universal quantitative dependence. The study showed that a mathematical model built on the basis of these principles resulted in the emergence of new generalized concepts, logically combining the previously considered to be unrelated concepts of hydro- and thermal series introduced by V.R. Volobuev, the Vysotsky - Ivanov moisture coefficient and the radiation dryness index by M. Budyko. In addition, the simulation showed that the concepts elucidating the indicator of the radiation energy utilization by biogeocenosis were represented by the interrelated coefficients of the heat and precipitation utilization in soils. The coefficients were also shown to have specific values for different soil-bioclimatic areas. On the basis of the new indicators, soils were grouped in such a way as to produce patterns essentially different in many details from the conventional grouping.
Conclusions. The new concepts represent a unified integral system, and the approach as a whole can be considered as an alternative physico-theoretical way to describe natural laws and regularities by using extreme (variational) methodology.
Key words: symmetry principle; optimality principle; system approach; hydrothermal coefficients; idealizations; mathematical model
How to cite: Chichulin A.V. Physico-theoretical basis of the mesoscopic approach to the study of soil and climatic regulations // The Journal of Soil and Environment. 2020. 3(2). e116. doi:10.31251/pos.v3i2.116 (in Russian with English abstract).
References
Abramova N.T. Reductionist tendencies of cybernetics In book: Cybernetics and dialectics. Moscow: Nauka, 1978, p. 287-306. (in Russian)
Agoshkova E.B., Akhlibinsky B.V., Fleishman B.S. Systemology: essence and place in scientific knowledge // Synergetics and methods of science. St. Petersburg: Nauka, 1998.S. 63-76. (in Russian)
Akchurin I.A. Unity of natural science knowledge. Moscow: Nauka, 1974.208 p.
Aseev V.A. Extremal principles in natural science and their philosophical content. Leningrad: Publishing House of Leningrad State University, 1977.232 p. (in Russian)
Akhromeeva T.S., Kurdyumov S.P., Malinetskiy G.G., Samarskiy A.A. Nonstationary structures and diffusion chaos. Moscow: Nauka, 1992. 544 p. (in Russian)
Bir G.L., Pikus G.E. Symmetry and deformation effects in semiconductors. Moscow: Nauka, 1972.584 p. (in Russian)
Bridgman P. Dimension Analysis. Izhevsk: Research Center "Regular and Chaotic Dynamics", 2001. 148 p. (in Russian)
Budyko M.I. Heat balance of the earth's surface. Leingrad: Gidrometeoizdat Publ., 1956.256 p. (in Russian)
Wigner E. Events, laws of nature, principles of invariance, Physics-Uspekhi,1965, Vol. 85, Issue 4, p. 727-736. (in Russian)
Wigner E. Incomprehensible effectiveness of mathematics in the natural sciences, Physics-Uspekhi, 1968, Vol.94, Issue 3, p. 535-546. (in Russian)
Volobuev V.R. On Soil-Climatic Areas, Pochvovedenie, 1945, No.1, p.3-16. (in Russian)
Volobuev V.R. Soils and climate. Baku, ed. Acad. Sciences Azerb. SSR., 1953. 320 p. (in Russian)
Volobuev V.R. Climatic conditions and soils, Pochvovedenie, 1956. No.4, p.24-37. (in Russian)
Volobuev V.R. Soil system of the world. Baku: ELM Publ., 1973, 308 p. (in Russian)
Volobuev V.R. Ecology of soils. Baku: Publishing House of the Academy of Sciences of Azerbaijan. SSR, 1963. (in Russian)
Volobuev V.R. Introduction to the energy of soil formation. Moscow: Nauka Publ., 1974. 128 p. (in Russian)
Gaponov-Grekhov A.V. Rabinovich M.I. Nonlinear Physics. Stochasticity and structures In book: Physics of the XX century. Development and prospects. Moscow: Nauka Publ., 1984, p. 219-280. (in Russian)
Heisenberg V. Physics and Philosophy. Part and whole. Moscow: Nauka Publ., 1989, 400 p. (in Russian)
Gladyshev G.P. Thermodynamics and macrokinetics of natural hierarchical processes. Moscow: Nauka Publ., 1988, 287 p. (in Russian)
Glazovskaya M. A. General soil science and soil geography. Moscow: High School Publ., 1981, 400 p. (in Russian)
Globus A. M. Soil and hydrophysical support of agroecological mathematical models. Leningrad: Gidrometeoizdat Publ., 1987, 427 p. (in Russian)
Globus A.M. Physics of non-isothermal intrasoil moisture exchange. Leningrad: Gidrometeoizdat Publ., 1983, 278 p. (in Russian)
Gukhman A. A. Introduction to the theory of similarity. Moscow: Higher School Publ., 1973, 296 p. (in Russian)
Davis P. Superpower. The search for a unified theory of nature. Moscow: Mir Publ., 1989, 272 p. (in Russian)
Dobrovolsky G.V. Philosophical aspects of genetic soil science, Pochvovedenie, 2004. No 8, p. 901-910. (in Russian)
Dobrovolsky G.V., Urusevskaya I.S. Geography of soils. Moscow: Publishing House of Moscow State University. 2004, 460 p. (in Russian)
Druzhininin D.L., Vanyarkho V.G. Synergetics and methodology of system research In book: System Research. Moscow: Nauka Publ., 1989. p. 283-303. (in Russian)
Dyshleviy P.S. Evolution of "principles of description" in physical knowledge In book: Philosophical foundations of natural sciences. Moscow: Nauka Publ., 1976, p. 91-117. (in Russian)
Zaslavsky G.M., Sagdeev R.Z. Introduction to nonlinear physics. From a pendulum to turbulence and chaos. Moscow: Nauka Publ., 1988, 368 p. (in Russian)
Konopelchenko B.G., Rumer Yu.B. Atoms and hadrons. (Classification problem), Physics-Uspekhi, 1979, Vol. 129, Issue 2, p. 339-345. (in Russian)
Kulakov Yu.I. Classification of chemical elements on a new basis In book: Classical natural science and modern science. Novosibirsk. Publishing House NSU, 1991, p. 97−118. (in Russian)
Kulakov Yu.I. The theory of physical structures. Novosibirsk: Publishing house "Alpha Vista", 2004. 851 p. (in Russian)
Landau L.D., Lifshits E.M. Quantum mechanics. Non-relativistic theory. Vol.3. Moscow: Nauka Publ., 1989, p. 768. (in Russian)
Lyubarsky G.Ya. Group theory and physics. Moscow: Nauka Publ., 1986, 224 p. (in Russian)
Michurin B.N. Energetics of soil moisture. Leningrad: Gidrometeoizdat Publ., 1975, 141 p. (in Russian)
Neimark Yu.I., Landa P.S. Stochastic and chaotic oscillations. Moscow: Nauka Publ., 1987, 424 p. (in Russian)
Nicolis G., Prigogine I. Cognition of the Complex. Introduction. Moscow: Mir Publ., 1990, 344 p. (in Russian)
Ovchinnikov N.F. Principles of conservation. Conservation laws. Symmetry. Structure. Moscow: Book House "LIBROKOM", 2009, 336 p. (in Russian)
Ovchinnikov N. F. Principles of theorizing knowledge. Moscow: Institute of Philosophy, Russian Academy of Sciences, 1996, 215 p. (in Russian)
Ovchinnikov N. F. The trend towards the unity of science. Moscow: Nauka Publ., 1988, 272 p. (in Russian)
Onishchenko V.G. Similarity of thermodynamic characteristics of soil moisture and their generalized description. Abstract dis. Doctor of Agricultural Sciences. Moscow, 198, 48 p. (in Russian)
Pachepskiy Ya.A. Mathematical models of physical and chemical processes in soils. Moscow: Nauka Publ., 1990, 188 p. (in Russian)
Poluektov R.A., Smolyar E.I., Terleev V.V., Topazh A.G. Models of the production process of agricultural crops. Publishing house of St. Petersburg University, 2006, 396 p. (in Russian)
Preobrazhensky N.G. Heuristic nature of symmetry properties in physics In book: Methodological problems of mathematical physics. Novosibirsk: Nauka, Sib-e department, 1986, p. 232-245. (in Russian)
Razumovskii O.S. Group theory In book: Methodological problems of mathematical physics. Novosibirsk: Nauka Publ., Siberian Brunch, 1986, p. 225-231. (in Russian)
Rosen R. Optimality principle in biology. Moscow: "Mir" Publ., 1969, 216 p.
Rumer Yu. B., and Fet A.I., The Spin (4) group and the periodic table, Theoret. and Math. Phys, 1971, Vol. 9, No.2, p. 1081–1085. (in Russian)
Sadovskiy V.N. Foundations of the general theory of systems. Logical and methodological analysis. Moscow: Nauka Publ., 1974, 280 p. (in Russian)
Sedov L.I. Similarity and Dimension Methods in Mechanics. Moscow: Nauka Publ., 1981, 448 p.
Sirotenko O.D. Mathematical modeling of water-thermal regime and productivity of agroecosystems. Moscow: Gidrometeoizdat Publ., 1981, 166 p. (in Russian)
Sokolov I.A. Theoretical problems of genetic soil science. Novosibirsk: "Humanitarian technologies", 2004, 288 p. (in Russian)
Tanasienko A.A., Chumbaev A.S. Yakutina O.P. Miller G.F. Conditions and intensity of erosion-accumulative processes in the Pre-Salair region, Pochvovedenie, 2013, No, 11, p.1397-1408. (in Russian)
Topazh A.G. Dynamic Productivity Models: Dead End or Crossroads? SPb .: AFI Publ., 2014.S. 48-69. (in Russian)
Urmantsev Yu. A. Symmetry of nature and the nature of symmetry. Philosophical and natural science aspects. Moscow, 1974, 229 p. (in Russian)
Uskov I.B., Moiseev K.G. Development of modeling with the application of theory and methods of similarity in agrophysics, Agrofizika, 2018, No. 1, p. 53-63. (in Russian)
Feynman R. The nature of physical laws. Moscow: Nauka Publ., 1987.160 p. (in Russian)
Chichulin A.V. Methodological analysis of the conceptual framework in soil ecology, The Journal of Soils and Environment, 2019, Vol. 2, No.3, e89. (in Russian)
Received 17 October 2020; accepted 26 November 2020; published 27 November 2020
About the author:
Chichulin Alexander V. – Candidate of Biological Sciences, Senior Researcher in the Laboratory of Soil Physical Processes in the Institute of Soil Science and Agrochemistry of the Siberian Branch of the Russian Academy of Sciences (Novosibirsk, Russia); chichulin@issa-siberia.ru
The author read and approved the final manuscript
 The article is available under Creative Commons Attribution 4.0 License
The article is available under Creative Commons Attribution 4.0 License

