Оргинальная статья

МЕТОДОЛОГИЧЕСКИЙ АНАЛИЗ ПОНЯТИЙНОГО АППАРАТА В ЭКОЛОГИИ ПОЧВ

А.В. Чичулин

Адрес: ФГБУН Институт почвоведения и агрохимии СО РАН, проспект Академика Лаврентьева, 8/2, г. Новосибирск, 630090, Россия

Методология. Проведен методологический анализ и выяснены причины ограниченной применимости при решении ряда задач в экологии почв традиционных климатических гидротермических коэффициентов – радиационного индекса сухости Будыко и коэффициента увлажнения Высоцкого-Иванова.

Результаты. На основе анализа размерности, примененного к задаче о зависимости характера почвенного покрова от гидротермических условий введены новые понятия - безразмерные критерии подобия, играющие роль почвенно-климатических коэффициентов и обладающие более широким диапазоном применимости по сравнение с традиционными климатическими гидротермическими коэффициентам. Показано, что связь между традиционными климатическими и новыми почвенно-климатическими гидротермическими коэффициентами носит асимптотический характер. Используя эмпирическое уравнение М. И. Будыко для испарения почвенной влаги и новые почвенно-климатические коэффициенты, получено уравнение "почвенно-климатической характеристики" (ПКХ), учитывающее совместное влияние климатических характеристик (средние многолетние значения радиационного баланса R и осадков P) и свойств почвенного субстрата (испарение почвенной влаги E(R,P)) на особенности почвообразовательного процесса.

Заключение. В отличие от традиционного подхода, упорядочивающего почвенные свойства на эмпирической климатической основе, новый физико-теоретический подход обладает возможностью теоретического предсказания ряда системных почвенных закономерностей, в частности - группировки почв на аридный, гумидный и сбалансированный педокосмы.

Ключевые слова: экология почв; принципы симметрии; принцип дополнительности; гидротермические коэффициенты; идеализации; математическая модель

Цитирование: Чичулин А. В. Методологический анализ понятийного аппарата в экологии почв // Почвы и окружающая среда. 2019. Том 2. № 3. e84. 10.31251/pos.v2i3.89

"С давних времен, с тех пор, как существует зучение природы, оно имело перед собой в качестве идеала конечную, высшую задачу: объединить пестрое многообразие физических явлений в единую систему, а если возможно, то в одну-единственную формулу".

Макс Планк (1966)

Наука в своем развитии неизбежно встречается с теоретико-познавательными и методологическими проблемами, решение которых требует переосмысления сложившегося понятийного аппарата и разработки новых математических методов. В естествознании эти проблемы выражаются в возникновении противоречий между старыми теоретическими представлениями (понятиями, законами, теориями) и новыми объективно установленными фактами. Основной причиной появления таких противоречий, является то, что процесс формирования понятий всегда включает в себя определенные процедуры абстрагирования и идеализаций. Например, в почвоведении, в силу объективной сложности и относительно слабой изученности объекта исследования, при количественном описании специфических почвенных закономерностей зачастую довольствуются соглашениями о выборе в качестве соответствующих эталонов (масштабов соотнесения), характеристик обособленных факторов почвообразования, которые в отрыве от остальных, лишь приблизительно отражают системный характер почвенных феноменов. Будучи в определенной мере оправданными на начальном, эмпирическом этапе исследования, эти соглашения, тем не менее, неосознанно замыкают его в упрощенные теоретические рамки, которые рано или поздно, неизбежно становятся тесными, приводят к логическим противоречиям и, как следствие, к необходимости решения вопроса об определении границ применимости используемых понятий и методов, что принципиально возможно только в рамках нового, более широкого теоретического подхода.

В качестве примера, обратим внимание на важное различие современной физики и почвоведения как теоретических систем. Если понятия физики в большинстве случаев строго определены и имеют свое математическое выражение, так, что между ними мы имеем четко обозначенные логические связи, позволяющие из одних знаний выводить другие,  то сказать все это про современное почвоведение пока еще нельзя. Неадекватное осознание связей между элементами почвенного знания приводит к тому, что до сих пор большая часть понятий, используемых в почвоведении, представляет собой, используя известное выражение А. Эйнштейна, каталог, а не систему.

Резюмируя вышесказанное, мы утверждаем, что причиной методологических и теоретических проблем в современном генетическом почвоведении, зачастую выступает использование упрощенных, не системных понятий и методов при изучении принципиально системных характеристик сложных природных объектов. Ранее, в работах (Чичулин, Елизарова, 2004; Чичулин Дитц, 2008; Чичулин, 2010; Чичулин, Шапорина, 2016) на примерах из гидрофизики и экологии почв, мы уже пытались рассмотреть некоторые аспекты этой общей проблемы.

1) в гидрофизике почв при построении влажностной характеристики почв - зависимости потенциала почвенной влаги от ее влажности ψ(ϑ) за нулевой уровень потенциала принимается потенциал свободной влаги. За рамками теоретического описания в этом случае оказывается прямой учет влияния структуры твердой фазы почвы на содержащуюся в ней влагу;

2) в экологии почв, при изучении структуры почвенно-биоклиматических ареалов, используются различные климатические гидротермические коэффициенты (Добровольский, Урусевич, 2004), которые в своих прямых определениях, учитывая совместное действие только тепла и влаги, не учитывают, что это взаимодействие всегда происходит в конкретном почвенном субстрате. Степень оправданности такого рода допущений и вытекающие из них следствия, как правило, вообще не анализируются. Между тем, все факторы почвообразования, взаимодействуя между собой и, влияя на сущность и направление почвообразовательного процесса, действуют вместе как система взаимосвязанных элементов (Ковда, 1973). Совершенно естественно, что это ограничение определенным образом отражаться и на результатах исследования.

В настоящей работе мы, по возможности детально, рассмотрим задачу из области экологии почв, методологический анализ и теоретическое решение которой требуют более глубокого, чем обычно принято, учета взаимосвязей между почвенно-климатическими характеристиками. Речь идет о задаче количественного описания структуры почвенно-климатических ареалов в зависимости от гидротермических условий.  Актуальность работы обеспечивается тем, что в настоящее время существуют не только эмпирические, но и фундаментальные физико-теоретические принципы, на основе которых можно предложить конкретный подход к решению этой задачи. Мы опишем метод построения универсальной математической зависимости, выступающей в роли новой системы координат для любых почвенных характеристик, в частности − и для описания структуры почвенно-климатических ареалов. Эту зависимость для определенности далее будем называть почвенно-климатической характеристикой (ПКХ) и дадим ее интерпретацию. Метод основан на применении к задаче анализа размерности (Гухман, 1973; Седов, 1981; Кутателадзе, 1982), который, с целью подчеркнуть наше убеждение в его фундаментальной роли, которую он должен играть в решении задач современной экологии почв, будем называть принципом симметрии (инвариантности), имея в виду аналогию с общим подходом к решению проблем теоретической физики 20 века. В качестве экспериментальной базы данных, анализируемых в рамках нового теоретического подхода, использован материал, собранный и частично обработанный В. Р. Волобуевым (1945; 1953; 1956; 1963).

Таким образом, конкретной целью настоящей работы является разработка физико-теоретического подхода в экологии почв, в основе которого лежат новые понятия почвенно-климатических гидротермических коэффициентов, учитывающих совместное действие радиационного баланса, осадков и свойств почвенного субстрата в формировании специфики почвообразования. Для достижения этой цели необходимо решить следующие задачи:

1. Провести методологический анализ идеализаций, лежащих в основе традиционных гидротермических коэффициентов (радиационного индекса сухости Будыко и коэффициента увлажнения Высоцкого-Иванова) и, как следствие этого, выявить причины ограниченной применимости разработанных с их использованием исследовательских методов в современной экологии почв.

2. На базе фундаментального принципа симметрии (анализа размерностей), обеспечиваю-щего общий физико-теоретический подход к проблеме, определить в форме безразмерных критериев подобия новые, более широкие, по сравнению с традиционными, понятия почвенно-климатических гидротермических коэффициентов.

3. Проанализировать связи, носящие асимптотический характер, между традиционными климатическими и новыми почвенно-климатическими гидротермическими коэффициентами.

4. Из уравнения испарения почвенной влаги М. И. Будыко, с использованием новых почвенно-климатических коэффициентов, вывести уравнение (модель), описывающее совместное действие климатических и субстратных характеристик на специфику почвообразовательных процессов.

5. Показать отличие результатов, вытекающих из моделей, полученных с помощью традиционных и новых гидротермических понятий.

Прежде чем перейти к конструктивной части настоящей работы, сделаем важное с нашей точки зрения замечание. Как ясно из вышеизложенного, работа в значительной степени носит критико-аналитический характер в отношении некоторых традиционных понятий, используемых в экологии почв. Чтобы не сложилось впечатление, что подобная позиция является исключительной, приведем мнения некоторых ведущих ученых о теоретическом и методологическом состоянии исследований в современном генетическом почвоведении в целом, необходимости и перспективах их дальнейшего развития.

И.А. Соколов (2004): "В настоящее время былая слава и былая роль генетического почвоведения в значительной степени утрачены. ..."тихий погром" в генетическом почвоведении остался почти незамеченным, ... деградация почвоведения снова до уровня только сельскохозяйственной науки началась с перевода Почвенного института им. В. В. Докучаева в ВАСХНИЛ.... Фундаментальная наука была вновь возвращена на додокучаевский уровень и сведена до одной из своих прикладных ветвей".

Г.Ф. Хильми (1968): "Как бы ни было велико значение идей Докучаева, Воейкова, Вернадского и других классиков широкого мышления о природе, в наше время этих идей далеко недостаточно и требуется их серьезное развитие в принципиально новых направлениях. Свойственное географии комплексное мышление о биосфере и географической оболочке необходимо дополнить современными представлениями, и прежде всего энергетико-кибернетическим подходом".

Ограничимся этими высказываниями.

Прежде всего отметим, что естественным научным методом выбора масштаба измерений считается принятие в качестве эталона какого-либо устойчивого природного процесса. Например - еще на заре цивилизации такой подход интуитивно проявился в определении мер времени по наблюдениям за периодичностью вращения Земли вокруг своей оси и вокруг Солнца. Высокую степень универсальности таких астрономических часов подтвердила практика. Однако, принятые стандарты никогда не бывают абсолютно приемлемыми для всех реальных ситуаций. Так, в случае изучения системного, многофакторного и иерархического природного явления, к которым безусловно относится и почва, решение вопроса о выборе эталонов часто оказывается не однозначным. На начальном, эмпирическом этапе изучения представляется естественным, что для различных характеристик такого явления можно принять также различные, не связанные между собой, соглашения о соответствующих системах отсчета. Однако с каждым соглашением всегда связана определенная совокупность идеализирующих допущений, причем их осознанная и явно сформулированная часть, как правило,  мала по сравнению с неявно подразумеваемой частью. Эти неявно подразумеваемые допущения, относительно безвредные в условиях изолированного применения каждого соглашения, проявляются в виде логических противоречий в случае попыток их объединения, когда необходимо одновременно использовать несколько взаимоисключающих идеализированных понятий. В этом случае и возникает задача нахождения условий логической совместимости различных допущений. История развития научных направлений подтвердила,  что достигается это в результате методологического анализа исследовательских процедур и, в случае удачного решения такой задачи, разрабатывается система новых понятий, лежащая в основе более широкой и адекватной теории сложного явления.

Приведем два хорошо известных примера:

1) Физика, как наиболее развитая в экспериментальном и теоретическом отношениях наука, еще в начале 20 в. пришла к необходимости пересмотра классических понятий пространства, времени, дискретности, непрерывности. Произошло это в процессе методологического анализа противоречий, возникших между новыми экспериментальными результатами и теоретическими положениями в классической механике, термодинамике и электродинамике. Разрешение этих противоречий, привело к появлению величайших теорий современности - теории относительности и квантовой механики, ограничивших применимость понятий классической механики. 

2) Открытие нерегулярных колебаний в диссипативных системах различной природы (физических, химических, биологических, экономических) стало одной из крупнейших научных сенсаций в 60 - 70-е годы 20 в. Оно потребовало переосмысления роли понятий устойчивости и неустойчивости в макроскопических процессах, что привело к пересмотру фундаментальных представлений о природе. На этой основе оформилась дисциплина, которую в настоящее время называют по-разному − нелинейная физика, физика диссипативных структур, синергетика и др. Все они с единой точки зрения описывают процессы появления качественно новых явлений (самоорганизации) в сложных системах различной природы. При этом общую причину этих процессов видят в учете более тонких, нелинейных особенностей системных взаимосвязей.

Открытие В. В. Докучаевым нового понимания почв как особых природных тел, позволило ему заложить основы новой фундаментальной научной дисциплины - генетического почвоведения, в становлении которой важную роль сыграли общие методологические принципы изучения природы - системности, целостности, закономерных связей составляющих ее элементов. Именно методологический принцип изучения связей между почвой, с одной стороны, и комплексом всех природных экологических условий - с другой, стал основой генетического почвоведения. Однако правомерен вопрос: насколько последовательно реализуется этот принцип в современных почвенно-экологических исследованиях?

С самого начала разработки основ генетического почвоведения почвоведы уделяли большое внимание характеристике климатических условий почвообразования. В частности, с целью нахождения количественных корреляций между типами теплового и водного режимов и закономерностями распространения почв на земной поверхности, были введены различные гидротермические коэффициенты. В работе рассматриваются два из них - введенный, по предложению В. В. Докучаева, еще в 1904 г. коэффициент увлажнения Высоцкого-Иванова и радиационный индекс сухости, определенный М. И. Будыко в 1948 г. Причина выбора именно этих коэффициентов заключается в том, что их теоретический анализ подкреплен и необходимой базой эмпирических данных. Даты первого определения этих коэффициентов приведены специально, с целью подчеркнуть длительность их применения в неизменной форме. Прежде всего, дадим им строгие определения.

Безразмерный коэффициент увлажнения Высоцкого-Иванова

показывает в какой мере выпадающие в данном регионе осадки возмещают испаряемость и получается от деления среднегодовой суммы осадков Р [мм] на возможную испаряемость с водной поверхности по эвапорометру Е₀ [мм].         

Безразмерный радиационный индекс сухости Будыко

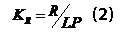
отражает возможность накопления влаги при данных условиях и определяется как отношение между радиационным балансом территории R [ккал см^-2 год] и годовой суммой осадков Р, выраженной в калориях скрытой теплоты парообразования, где L [кал см^-3] - скрытая теплота парообразования, для определенности принятая в работе равной 600 [кал см^-3] = 0.06 [ккал мм^-1] (Реймерс, 1990). Обратим внимание, что в обоих определениях используется понятие потенциально-возможной (иными словами - максимально возможной) величины: в одном случае − испарения с водной поверхности, во втором случае - испарения всех осадков.

Начиная с 1945 г. В. Р. Волобуев обращал внимание на неправомерность противопоставления двух точек зрения по вопросу о том, какие данные следует принимать во внимание при изучении почвенно-климатических соотношений - данные по атмосферному или собственно почвенному климату. Он подчеркивал, что совершенно бесспорна необходимость изучения почвенного климата как свойства почвы, но столь же правомерна и другая задача - исследование закономерных соотношений между почвой и средой ее формирования, в качестве которой может выступать и атмосферный климат. Эти закономерные соотношения наиболее естественным образом разъясняются путем исследования связей между атмосферным и почвенным климатом. При общей постановке проблемы, такой подход следует признать совершенно правильным, но только при условии, если соответствующие параметры атмосферного климата выступают в роли естественных граничных условий для формирования почвенного климата. Исследования В. Р. Волобуева в этом направлении неоднократно детально описаны, поэтому мы не будет специально заострять на них внимание (Волобуев, 1963; 1973; 1974).

Однако необходимо подчеркнуть, что эти исследования В. Р. Волобуева базировались на использовании коэффициента увлажнения K_P (1) и именно в этом пункте могут быть подвергнуты критике. Дело в том, что связи между атмосферным и почвенным климатом действительно могут быть согласованы между собой, но только в том случае, если параметры атмосферного климата представлены в определенной форме - в форме граничных условий, задающих условия взаимодействия почвы с внешней средой. Коэффициент увлажнения в той его части, которая относится к выбору масштаба соотнесения - переменной, расположенной в знаменателе (1), этим условиям не удовлетворяет. Заметим, что K_P определен в форме безразмерного параметра, а чтобы такой параметр имел физический смысл меры отношения интенсивностей двух процессов, протекающих в почве (или на ее границе), необходимо сравнивать эти процессы в одно и тоже время и в одном и том же месте, причем именно почвы (поверхности), а не водоема. Процессы испарения с поверхностей почвы и водоема не соизмеримы, а если их все-таки приходится сопоставлять между собой, то это означает, что мы используем более абстрактную, более грубую, не учитывающую определенной почвенной специфики, теоретическую схему. То есть, в таком случае, за универсальность (независимость от Р) и экспериментальную простоту измерения традиционного коэффициента увлажнения приходится расплачиваться определенной ценой - потерей представлений о структуре почвенного субстрата (они заменяется представлениями об однородной водной толщи).

Подытожим вышесказанное: коэффициент увлажнения Высоцкого-Иванова в определенном смысле является грубым, предельно идеализированным понятием и по этой причине принципиально не может отразить всю возможную на данном уровне исследования почвенную специфику. Справедливости ради отметим, что Волобуев В. Р. (1974) отметил этот факт. Он писал: "Представляется оправданным при исследовании ландшафтов сравнивать условия, складывающиеся в самих ландшафтах, и на этой основе устанавливать известные градации их признаков, чем брать в качестве эталона не ландшафт, а "водную поверхность". К сожалению В. Р. Волобуев не довел до логического конца эту абсолютно правильную мысль и ограничился тем, что заменил "водную поверхность" - "ландшафтом в условиях высокого природного увлажнения" (при осадках P = 1600 мм за год). По существу, произведя в уравнении (1) следующую замену:

то есть, заменив одну постоянную величину другой постоянной величиной, В. Р. Волобуев не внес принципиальных, качественных изменений в традиционный коэффициент K_P, а ограничился лишь небольшой количественной поправкой к нему. Тогда как последовательный подход требует замены испарения с поверхности свободной влаги E(R) (рис.1С) испарением с поверхности почвы E(R,P) (рис.1В). В принципиальном отношении все вышесказанное о коэффициенте увлажнения (1), относится и к радиационному индексу сухости (2), с поправкой на то, что его расчетная формула (2) предполагает, что осадки испаряются полностью, образно говоря - даже не долетая до поверхности почвы (рис.1А).

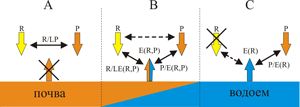
Рисунок 1. Общая схема задачи и три варианта выбора масштабов (эталонов) сравнения для традиционных и новых гидротермических коэффициентов. В качестве независимых переменных рассматриваются радиационный баланс земной поверхности R и среднегодовые осадки P. Испарение - зависимая переменная, может происходить двумя способами - с поверхности почвы E(R,P) или свободной воды E(R) (эвапорометр, естественный водоем). Эти два случая описываются разными зависимостями. Схемы образования различных коэффициентов: (А) - классического гидротермического коэффициента R/LP - радиационного индекса сухости Будыко М.И., где L - скрытая теплота парообразования; (В) – новых обобщенных переменных, безразмерных критериев подобия R/LE(R,P) и P/E(R,P). В этом варианте влажность почвы является переменной величиной, зависящей от P, чем отличается от вариантов (А и С); (С) - классического коэффициента увлажнения Высоцкого – Иванова P/E(R). Черные сплошные стрелки обозначают прямой учет связи между переменными, пунктирные - косвенный. Перечеркнутые стрелки означают, что в данном варианте параметры, обозначаемые ими, в явном виде не учитываются.

На (рис.1) приведены три схемы, поясняющие связь между различными климатическими и почвенными переменными при определении традиционных (А и С) и новых (В) гидротермических коэффициентов. В случае радиационного индекса сухости (А), в качестве масштаба соотнесения для радиационного баланса R берется среднегодовая сумма осадков P умноженная, для соблюдения размерности на скрытую теплоту парообразования L. Обратим внимание, что хотя сама почва не фигурирует в этом понятии, как было сказано выше - осадки испаряются, не долетая до поверхности почвы, формально это все-таки эквивалентно условию, что все осадки полностью испаряются именно из почвы при условии высокого радиационного баланса:

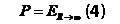
Это замечание важно потому, что помогает на уровне физической картины изучаемого явления, обосновать необходимость выбора именно функции испарения из почвы E(R,P) в качестве единой меры (единого масштаба соотнесения, единого эталона) и для радиационного баланса R и для осадков P. Этим одновременно определяются как критерии подобия, играющие роль новых почвенно-климатических коэффициентов, так и через общий масштаб устанавливается между ними связь.

Таким образом, можно утверждать, что первый традиционный гидротермический коэффициент - радиационный индекс сухости Будыко K_R, определяется и потому полностью применим в предельной ситуации - полного испарения всей влаги из почвы, при котором почва остается абсолютно сухой.

Второй традиционный гидротермический коэффициент – коэффициент увлажнения Высоцкого-Иванова K_P определяется в противоположной предельной ситуации – полного увлажнения почвы, вплоть до образования на ее поверхности свободной влаги (водоем или эвапорометр). Следовательно, уравнения (1) и (2) мы можем заменить тождественными им уравнениями:

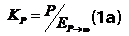
В такой записи становится очевидной симметрия между традиционными коэффициентами.

Следующий логический шаг - переход в знаменателях уравнений (1а) и (2а) к единой функции испарения E(R,P), зависящей и от осадков P и от радиационного баланса R, причем с выполнением условий:

означающих, что традиционные величины различных испарений E входят в качестве соответствующих граничных условий в новую функцию E(R,P) - функцию испарения почвенной влаги. Таким образом, можно определить новые почвенно-климатические гидротермические коэффициенты, сконструированные в форме безразмерных критериев подобия:

В уравнениях (6) и (7) мы сохранили для новых коэффициентов обозначения, которые уже были использованы для традиционных коэффициентов (1) и (2), хотя в литературе для последних приняты другие обозначения: КУ и I_R соответственно. В настоящей работе использованы симметричные обозначения K_P и K_R потому, что они характеризуют различные проявления единого по своей физической сущности процесса. Поэтому, даже на уровне обозначений, считаем важным подчеркнуть элементы единства в новом подходе.  Полагаем, что путаницы не должно быть.

За каждой математической формулой стоит определенная концептуальная модель – наглядная физическая картина явления. В связи с этим, интересно отметить, что при желании можно усмотреть нечто символическое в аналогии последовательности смен физических картин явлений, описываемых относительно более простыми традиционными (формулы (1), (2) и (рис.1А, С) - испарение из почвы не учитывается) и более общими новыми коэффициентами (формулы (6), (7) и (рис.1В) - почвенное испарение учитывается), с последовательностью смен библейских картин мира. Так, в первый и второй дни творения, когда еще нет разницы между водой, которая под твердью и водой, которая над твердью, процесс испарения воды, если и происходит, то только находящейся в свободном состоянии. Именно такие процессы описывают традиционные гидротермические коэффициенты (1) и (2). В третий день творения произошло разделение воды, которая под твердью, на землю и моря и, следовательно, появилось испарение воды с поверхности почвы (Бытие, 1: 2–13), описываемое уравнением (8), а гидротермические коэффициенты приняли форму (6) и (7).

Попутно отметим, что и понятие подобия, являющееся ключевым при разработке исследовательского метода, впервые упоминается в Библии в седьмой день творения, в связи с появлением человека (Бытие, 1: 26). С нашей точки зрения такая тесная аналогия между картинами мира и методами его понимания, свидетельствует о наличии неизменной, проходящей через тысячелетия, инвариантной компоненте в логике изучения и описания природных явлений человеком.

Анализ размерности начинается с построения теоретической схемы задачи, выбора значимых переменных и построения из них безразмерных комплексов (обобщенных переменных). Схема задачи приведена на рисунке 1В.

Сам анализ размерности, как и все принципы инвариантности, относится к метатеоретическим утверждениям, которым должны соответствовать законы природы. Он нашел широкое применение в различных научных направлениях, имеющих дело с изучением сложных систем.  Особую плодотворность он демонстрирует в тех случаях, когда известен только перечень значимых переменных для данной задачи, а математическая постановка задачи вообще отсутствует, т.к. исследуемое явление настолько сложно, что для него еще нет удовлетворительной математической модели, либо, если модель есть, нахождение искомых закономерностей прямым путем встречает значительные технические трудности (Седов, 1981). Как правило, именно с такими задачами до сих пор приходится иметь дело в экологии почв, изучающей закономерности взаимосвязей почв с факторами среды. В этих случаях главную роль играют экспериментальные методы исследования, которые дают возможность установить конкретные опытные факты - перечень свойств и параметров, множество частных взаимосвязей между которыми описывает изучаемую систему в данном приближении к действительности. Методами анализа размерностей этим эмпирическим взаимосвязям может быть придана обобщенная форма и уменьшено число переменных, т.е. осуществлена определенная теоретизация исходного материала. В частности, если перечень переменных полон, можно путем сопоставления размерностей быстро установить общий характер функциональной зависимости, которая связывает данные величины.

Математический аппарат анализа размерности очень прост. Однако, даже длительный опыт его формального применения не может гарантировать от ошибок (Гухман, 1973). Причины заключаются в том, что необходимыми условиями применения анализа размерности являются глубокое понимание сущности изучаемого явления и наличие полного набора данных. В противном случае возможна неоднозначная или ошибочная интерпретация результатов. В целом анализ размерностей не является всемогущим методом и подчас его возможности оказываются ограниченными. Рассматриваемая в настоящей работе задача о структуре почвенно-климатических ареалов в гидротермическом пространстве, является с этой точки зрения удачным примером. При ее анализе существует возможность перейти от эмпирического к физико-теоретическому уровню строгости, и довести решение до конкретных количественных результатов. Это обеспечивается как существующими теоретическими методами (анализ размерности), так и благодаря предварительной работе В.Р.Волобуева (рис.2), собравшего и опубликовавшего достаточно полную базу данных о зависимости характера почвенного покрова от гидротермических условий, а также работе М. И. Будыко (рис.3), проделавшего аналогичную работу в отношении сбора, первичной обработки и вывода эмпирической формулы, связывающей испарение почвенной влаги с радиационным балансом и осадками. По-существу, можно сказать, что в настоящей работе, собраны вместе и системно организованы все вышеперечисленные компоненты.

Рисунок 2. Расположение почвенно-климатических общностей по В.Р.Волобуеву (1974): 1 - пески пустынь, 2 – сероземы, 3 – бурые почвы полупустынь, 4 – каштановые почвы, 5 – каштановые почвы Африки, 6 – черноземы, 7 – серые лесные почвы, 8 – подзолы и подзолистые почвы, 9 – бурые лесные почвы, 10 – почвы тундр, 11 – желтоземы, 12 - красноземы и латериты (12а – основной ареал, 12b – более редкое распространение), 13 - коричневые почвы сухих лесов и кустарников (Африка), 14 – черные почвы саванн и тропических прерий, 15 – светло-бурые почвы тропических полупустынь, 16 – красно-бурые почвы саванн.

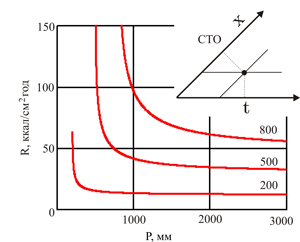
Рисунок 3. Изолинии испарения Е(R, P), рассчитанные по формуле Будыко М. И (выделены красным цветом). Одновременно рисунок иллюстрирует различные системы координат: декартова система координат − для независимых переменных R и P, аналогом является ортогональные оси независимых пространственной и временной переменных в классической механике. Изолинии испарения асимптотически сливаются с осями R и P. В этих предельных состояниях переменные R и P становятся независимыми. В настоящей работе изолинии испарения приняты за общий эталон в новой системе координат, криволинейность которой означает, что действуя одновременно в почве, процессы тепло-влагообмена почвы с атмосферой и испарения почвенной влаги становятся принципиально зависимы друг от друга и их нельзя рассматривать по отдельности. Врезка в правом верхнем углу, приведенная в качестве примера для сравнения, изображает систему координат в специальной теории относительности (СТО). В этой системе координат оси пространственной X и временной t переменных не ортогональны, поскольку в отличие от классической механики, в СТО эти переменные зависят друг от друга. Смысл иллюстрации заключается в демонстрации того, что, исходя из поставленной цели, системы координат могут быть выбраны не только декартовыми, а зависеть от конкретной задачи. Выбор не декартовой системы координат означает, что между используемыми переменными существуют взаимосвязи, которыми нельзя пренебречь.

Из соображений симметрии вытекает, что законы природы и их математические модели, являясь отражением объективной реальности, в наиболее общих формулировках, не должны зависеть от выбора мер. Это означает, что взаимосвязи предпочтительнее искать между безразмерными величинами. В нашей задаче определяющими переменными являются следующие величины: радиационный баланс земной поверхности R [кал/см² год], годовое количество осадков P [мм] и суммарное физическое испарение и транспирация почвенной влаги E [мм]. Поскольку процесс связан с испарением почвенной влаги, то в число определяющих величин должен входить параметр - скрытая теплота парообразования L = 589 кал/см³. Таким образом, общее число переменных m=4. При этом, существуют только две независимые (первичные) размерности: [кал] и [мм], то есть, n = 2.

В анализе размерности доказывается так называемая π - теорема, утверждающая, что число безразмерных комплексов p, которые могут быть составлены из заданного набора размерных величин, определяется формулой Бэкингема: p = m - n . (Сена, 1988). Таким образом, в нашем случае p = 2  . Другими словами, существуют только два безразмерных комплекса, связь между которыми будет в самом общем виде описывать структуру почвенно-климатических ареалов в гидротермическом пространстве. Легко показать, что их форма имеет вид R/LP и P/E.

π − теорема позволяет понять почему в задачах, использующих традиционные коэффициенты можно составить только по одному безразмерному комплексу. Причина заключается в том, что в обоих случаях используется неполный перечень значимых переменных. В случае расчета радиационного индекса сухости (рис. 1А) в явном виде отсутствует переменная, описывающая испарение почвенной влаги. Используются только переменные R, P и параметр L. В результате, из переменных можно составить только один безразмерный комплекс - R/LP. В случае расчета коэффициента увлажнения (рис.1С), радиационный баланс R учитывается только косвенно, в явной форме используются переменные P, E₀ и параметр L. Из них также можно составить только одну безразмерную комбинацию P/E₀.

Это объясняет причину, почему используя традиционные коэффициенты, графическое изображение результатов можно представить только в "смешаной" форме - когда на одной оси отложена безразмерная переменная, на другой − размерная (Волобуев, 1974; Реймерс, 1990). Нельзя утверждать, что это " абсолютно неправильно", существует смысл и в таком представлении результатов. Хотя этот вариант задачи в настоящей работе мы не рассматриваем, но в связи с ним, следует сделать принципиальное замечание, поскольку он свидетельствует не только о неполном теоретическом обобщении результатов. Дело в том, что почвенные закономерности нельзя выразить только в относительных (безразмерных) величинах, важную роль играют и абсолютные (размерные) значения переменных.  Можно сказать, что между относительными и абсолютными переменными складываются специфические отношения дополнительности - они отражают различные, но дополняющие друг друга зависимости. С учетом сказанного, энергетический подход В. Р. Волобуева следует отнести к промежуточному или смешанному подходу.

На (рис.4) для сравнения приведены данные о структуре почвенно-климатических ареалов, рассчитанные нами с использованием промежуточного - "смешанного" подхода В. Р. Волобуева (рис.4А) и полученные с помощью полностью "безразмерного" подхода - с использование новых почвенно-климатических коэффициентов (рис.4В). Аналогичные данные, приведенные на (рис.9) в работе И. А. Соколова (2004) в системе координат "сумма температур - коэффициент увлажнения", по - существу такие же, как в случае (рис.4А). Очевидно, что степень обобщения экспериментальных результатов является максимальной в "безразмерном" случае (рис.4В) – все данные о границах почвенно-климатических ареалов располагаются на одной линии, которая описывается универсальным уравнением, тогда как с помощью одного традиционного коэффициента увлажнения всегда получается развернутая структура (А), универсальное уравнение для которой будет рассмотрено в отдельной работе.

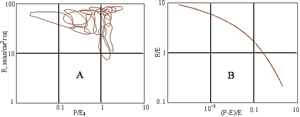
Рисунок 4. Расположение почвенно-климатических ареалов в разных системах координат: (А) – "смешанный" вариант В. Р. Волобуева (1974); (В) – "безразмерный" вариант, в котором за координаты приняты новые почвенно-климатические коэффициенты, введенные в настоящей работе. В случае (В) границы всех почвенно-климатических ареалов, рассчитанные по отдельным точкам (примерно 30 - 40 точек для каждого ареала), перекрывая друг друга, сливаются в одну криволинейную зависимость. Очевидна более высокая степень обобщения одних и тех же экспериментальных результатов, представленных в "безразмерной" форме.

Конечной целью анализа размерности является определение структуры характерных для исследуемого процесса обобщенных переменных - уравнения (6) и (7). Решением этой задачи его возможности исчерпываются. Вид функции в конечном выражении для функциональной зависимости между обобщенными переменными средствами анализа размерности не определяется - это исключено принципиально. Средства, с помощью которых решение может быть доведено до конкретной математической модели, надо искать за его пределами. В нашем случае мы воспользуемся эмпирическим уравнением Будыко М. И. для испарения почвенной влаги:

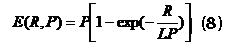
По поводу уравнения (8) следует сделать замечание. Оно, безусловно основано на определенных идеализациях и, с нашей точки зрения, может быть названо моделью "идеального почвенного испарения", играя роль, аналогичную модели "идеального газа" или "материальной точки" в физике. Оно является одним из простейших уравнений, но, тем не менее, отражает специфические особенности испарения почвенной влаги - испарение из капиллярно пористой структуры, а не из однородной толщи свободной влаги. В частности - оно учитывает этап падающей скорости испарения при отступлении капиллярной влаги вглубь пористого тела. Вместе с тем оно является линейным, позволяя разделить переменные и именно в связи с этим, получить искомое решение нашей задачи - уравнение ПКХ, в явном, аналитическом виде. Наконец, модель М. И. Будыко обладает свойством "глобальности" – во всем диапазоне изменения почвенно-климатических переменных масштаб отнесения для коэффициентов (6) и (7) хотя и является переменной величиной, но выражается одной и той же функцией E(R,P).

Поскольку все необходимые определения приведены, можно сформулировать основное "физико-теоретическое" противоречие, которое мы стремимся разрешить в нашей работе: определение (1), (2) и уравнение (8) логически не совместимы. В этом можно убедиться представив ситуацию, когда в (1) и (2) зафиксирован один из параметров R или P, а второй при этом варьируется. Применение уравнения (8) в этом случае сразу требует изменения фиксированного параметра. В противном случае нарушается условие инвариантности этого уравнения. Следовательно, задача заключается в том, чтобы так переопределить понятия гидротермических коэффициентов, чтобы они составляли с уравнением испарения почвенной влаги единую непротиворечивую систему. Легко убедиться, что уравнения (6), (7) и (8) этому условию удовлетворяют.

Существуют другие, более сложные, нелинейные эмпирические модели испарения, например, у В. Р. Волобуева (1974). По их поводу заметим, что на качественном уровне они приводят к результатам, аналогичным для модели М. И. Будыко, но не обладают ее основным преимуществом – простотой. Поэтому работать с ними можно только с помощью численных методов. Принципиально новые результаты, которые отличают их от "глобальной" модели М. И. Будыко, сводятся к эффекту "локальности" – добиться инвариантности функции ПКХ возможно, только варьируя показатель степени α(K_P) переменного масштаба отнесения 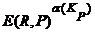. В настоящей работе этот вариант задачи не рассматривается.

С помощью ряда тождественных и чисто математических преобразований, которые мы здесь не приводим, уравнение М. И. Будыко (8) можно преобразовать к виду, в котором новые переменные – почвенно-климатические коэффициенты (6) и (7) разделяются. При этом интересно рассмотреть два случая, физический смысл которых заключается в подборе переменных, лучше всего коррелирующих с границами почвенных общностей (почвенно-климатических ареалов). В первом случае, с условным названием "неполного баланса", для упрощения введем следующие обозначения новых переменных:

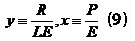
Тогда уравнение ПКХ будет выглядеть следующим образом:

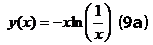
Этот вариант решения задачи нам представляется вполне вероятным для отдельных почвообразовательных процессов, хотя более определенный ответ требует дополнительного исследования. Также вероятным представляется вариант решения с явным учетом балансовых составляющих, связанных с испарением почвенной влаги, в тепло-влагообменных процессов взаимодействия почвы и атмосферы. В этом случае определим новые переменные следующим образом:

Тогда уравнение ПКХ выглядит так:

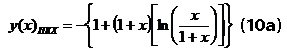
Принятые обозначения (9) и (10) отчасти поясняют смысл используемых условных названий в обоих случаях. Чтобы отличать различные уравнения ПКХ - (9а) и (10а) в (10а) использована подстрочная индексация.

На рисунке (5) приведены графики уравнений ПКХ для трех рассмотренных выше вариантов задачи – с традиционными климатическими (В) и новыми почвенно-климатическими коэффициентами (А) и (С). Видно, что основное отличие между ними заключается в том, что уравнение с традиционными коэффициентами имеет одну строго линейную ветвь, а оба уравнения с новыми коэффициентами имеют по две, ярко выраженные ветви с различными и переменными наклонами. Проинтерпретируем их с точки зрения теории подобия.

В случае (С), описываемом уравнениями (9) и (9а) - асимптотики функции ПКХ выходят либо на строго горизонтальную либо строго вертикальную зависимости. Это означает, что в каждом из этих двух предельных случаев происходит полное вырождение одного из критериев подобия - его влияние на описываемое явление стремится к нулю. Так, для горизонтальной асимптотики:

вертикальной асимптотики:

Другими словами - на почвы, находящиеся на горизонтальной асимптотике, перестают оказывать влияние осадки P, а на почвы, находящиеся на вертикальной асимптотике - радиационный баланс R. Для почвоведов ситуация станет понятнее, если, забегая несколько вперед, скажем что на горизонтальной асимптотике располагаются почвы гумидного, а на вертикальной - аридного педокосмов. В теории подобия такие области называются автомодельными. В этих областях из всех безразмерных комплексов, характеризующих описываемые явления, действенным остается только единственный. Все явления, попадающие в одну автомодельную область, подобны друг другу, отличаясь только масштабом. В случае (С) автомодельность является абсолютной, связанной с самой сутью рассматриваемого явления. Таким образом, аридные и гумидные почвы описываются разными безразмерными комплексами - разными наборами исходных переменных. В этом смысле можно говорить, что почвы различных педокосмов описываются разными почвенно-климатическими законами.

Строго говоря, распределение всех почвенно-климатических ареалов на кривой ПКХ является в значительной степени условным. Границы между ними настолько размыты, что скорее надо говорить о непрерывном переходе одного ареала в другой. Примечательно, что черноземный ареал (см. далее) всегда находится в области наиболее выраженного перегиба кривой ПКХ. И для случая (С) именно в области черноземов, наклон кривой ПКХ для случая "неполного баланса", наиболее приближен к наклону ПКХ для случая, описываемого традиционными коэффициентами.

В случае (А), описываемой формулами (10) и (10а) ситуация иная.         Испарение почвенной влаги здесь учитывается как компонента теплового и водного балансов почв. И случаев вырождения, аналогичных случаю (С) нет. Однако для гумидных почв проявляется область структурной автомодельности, в которой выполняется условие для составного критерия:

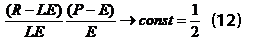
Интересно отметить, что в этом случае, когда испарение почвенной влаги учитывается в качестве одной из составляющих для теплового и водного балансов, сопоставление уравнений с традиционными (В) и новыми коэффициентами (А) приводит к физически осмысленному результату: в условиях высокого увлажнения эти уравнения асимптотически сходятся. Предполагая, что традиционные гидротермические коэффициенты, хотя и обладают ограниченной применимостью, все-таки отчасти отражают реальность, следует сделать вывод, что для различных почв границы почвенно-климатических ареалов лучше коррелируют с различными переменными, либо учитывающими балансы тепла и влаги, либо с "чистыми" радиационным балансом и осадками. Повторим, что случай (С) – коррелирует с (В) только в области почв со сбалансированного уровнем увлажнения (~ черноземы), что также должно иметь физический смысл. Отметим, что для аридных почв в случае (А) кривая ПКХ асимптотически не выходит на строгую горизонталь, свидетельствуя о том, что осадки продолжают оказывать влияние на процессы почвоообразования вплоть до полного их исчезновения.

Поскольку основные задачи настоящей работы заключаются в методологическом разборе с позиций анализа размерности понятийного аппарата, используемого в экологии почв и построении новой математической модели ПКХ, то и анализ полученных результатов в ней в значительно степени выглядит как проводимый с формальных позиций. Это неизбежное зло. Детальная интерпретация результатов выходит далеко за рамки анализа размерности. Но поскольку они безусловно представляют почвенно-экологический интерес, предполагается рассмотреть эти вопросы более подробно в отдельной работе.

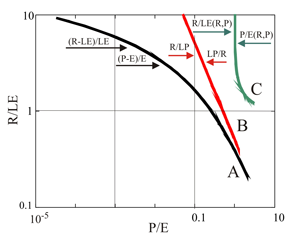
Рисунок 5. Сравнение уравнений для почвенно-климатических характеристик (ПКХ) для трех вариантов: (В) - уравнение связывает традиционные гидротермические коэффициенты; (А) – уравнение связывает переменные (10) в случае "полного баланса", (С) – уравнение связывает переменные (9) в случае "неполного баланса". Обозначения осей приведены только в общем воде. Конкретные переменные, в которых построены все уравнения ПКХ, приведены на рисунке возле каждой линии с привязками в виде стрелок соответствующего цвета.

По поводу уравнения ПКХ с традиционными коэффициентами (рис.5В) следует сделать следующее замечание. Как видно на рисунке (5), на графике с двойным логарифмическим масштабом оно представляет собой прямую линию – уравнение с постоянной симметрией во всем диапазоне изменения гидротермических условий. Неизменность симметрии в свою очередь означает, что все почвы, во всем диапазоне изменения параметров, подчиняются одному закону. Физический смысл этого результата заключается в том, что традиционные коэффициенты хотя и фиксируют простейшую связь между параметрами R и P, относящиеся к различным почвам, делают они это в предельно идеализированном случае. Эти коэффициенты являются слишком грубыми, чтобы чувствовать более тонкое системное различие между почвами. К тому же, поскольку эта прямолинейная зависимость получена с использованием уравнения Будыко (8), и переменные, которые описывают эту зависимость, строго обратно пропорциональны друг другу - R/LP и LP/R,

то ко всему вышесказанному об идеализациях, лежащих в основе уравнения Будыко, следует добавить, что оно не чувствует разницу между испарением "воды, которая над твердью" и "воды, которая под твердью" (Бытие, 1:7). Для этого уравнения - это одно и тоже состояние влаги.  Условно говоря, уравнение Будыко применимо к ситуации, описываемой в Библии в первый и второй дни творения. К тому же заметим, что любые два набора переменных x и y с помощью формальных преобразований y/x и x/y всегда сводятся к универсальной гиперболе y(x) = 1/x, которая сам, а по себе не отражает никакой качественной специфики исходных данных. Такая чрезмерная универсальность ставит слишком узкие теоретические рамки конкретным исследованиям. Именно поэтому, использование традиционных климатических гидротермических коэффициентов - радиационного индекса сухости Будыко и коэффициента увлажнения Высоцкого-Иванова, является во многих ситуациях слишком грубым приближением.

Таким образом, подчеркнем еще раз, главный недостаток традиционных коэффициентов в принципиальном плане заключается в том, что их применение не открывает никаких перспектив развитию специальных, более детальных почвенных теорий. Неоднократно подчеркивалось (Соколов, 2004), что почвенные закономерности не сводятся только к климатическим. И нашу модель (10а), построенную с помощью метода, расширяющего границы применимости гидротермических климатических коэффициентов можно рассматривать как конкретный аргумент в доказательстве неправомерности использования утрированной характеристики докучаевского почвоведения только как "климатического".

Повторим, что в отличие от линейного уравнения, изображенного на (рис.5В), уравнения ПКХ с новыми почвенно-климатическими гидротермическими коэффициентами (9а) и (10а) отличаются тем, что имеют криволинейный вид, с двумя ярко выраженными ветвями, описываемыми различными асимптотиками в противоположных диапазонах увлажнения – аридной и гумидной (рисунки 5, 6, 7). Эти асимптотики описываются однородными функциями с различной симметрией. Следовательно, почвы, находящиеся в различных (противоположных) гидротермических диапазонах, хотя и описываются одним уравнением, подчиняются различным законам подобия, связывающим переменные R, P и E.

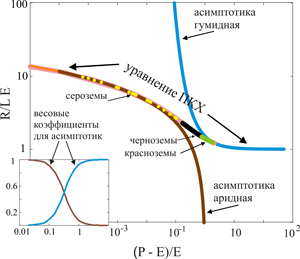
Рисунок 6. Расположение почвенно-климатических ареалов в обобщенных координатах (новых почвенно-климатических коэффициентах). На рисунке, чтобы избегнуть громоздкости, для примера разным цветом выделены экспериментальные данные только для ареалов сероземов (желтые точки), черноземов (черные точки - сливаются) и красноземов (зеленые точки), остальные почвы лежат на одной универсальной зависимости (светлокоричневая линия). В крайних положениях к ней асимптотически подходят две функции – гумидная асимптотика (синяя линия) и аридная асимптотика (темно-коричневая линия). Каждая точка на универсальной зависимости (КХП) в линейном приближении представима в виде суперпозиции (суммы) аридной и гумидной асимптотик с соответствующими весовыми коэффициентами, изображенными на врезке в левом нижнем углу (выделены тем же цветом, что и линии). Обратите внимание на отличие функций ПКХ на рисунке (6) от соответствующих функций на (рис. 5, 7), вызванных различием использованных переменных.

Легко показать из (10а), что эти асимптотики описываются следующими уравнениями:

Аридная асимптотика:

Гумидная асимптотика:

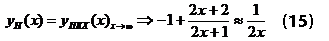
С их помощью любою точку на кривой ПКХ, а следовательно и любую почву, можно представить в виде суперпозиции:

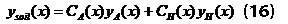
где функции С_A(x) и C_H(x) играют роль весовых коэффициентов для соответствующих асимптотик, вид которых приведен на врезке (рис. 6). Они отражают долю участия в процессе почвообразования аридной и гумидной составляющих.

Физический смысл представления точного уравнения ПКХ (10а) в приближенной форме (16) заключается не только в наглядности последнего. Это приближение носит принципиальный характер, поскольку именно в этом приближении строго определяются новые понятия аридных и гумидных почвенно-климатических ареалов. В "точных" уравнениях (9а) и (10а) таких понятий не существует. Естественная интерпретация приближенного уравнения (16) сводится к следующему. В общем процессе почвообразования действуют два глобальных закона симметрии (подобия), дополняющих друг друга - аридный и гумидный. Любая почва - обязательно представляется в виде комбинация того и другого, и только в асимптотическом пределе стремится к одному из них. В этом можно увидеть конкретное проявление методологического принципа дополнительности Н. Бора.

Отметим, что черноземные почвы, как и следовало ожидать, всегда находятся в месте перегиба функций ПКХ. Это лучше видно на графике первой производной от функции ПКХ (10а) по x (рис.7). Таким образом наша модель подтверждает точку зрения почвоведов, высказанную И. А. Соколовым (2004), о том, что в дополнении к аридному и гумидному педокосмам, есть все основания говорить о самостоятельности еще одного - мира почв сбалансированного увлажнения, который характеризуется неустойчивым сочетанием по большинству параметров. Это является естественным, поскольку мир почв сбалансированного увлажнения расположен в диапазоне переходного почвообразования, между аридным и гумидным педокосмами. Обратим внимание на то, что именно в этом диапазоне аридная и гумидная асимптотики резко расходятся, демонстрируя возрастающую неустойчивость.

На (рис.7) видно, что в принятой системе новых почвенно-климатических коэффициентов, на графике производной от функции ПКХ почвы аридного и гумидного педокосмов располагаются на прямых с различным углом наклона.

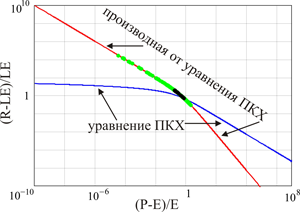
Рисунок 7. График уравнения ПКХ (10а) (выделен синим цветом) и график производной от уравнения ПКХ (выделен красным цветом). Из-за своей громоздкости, уравнение производной в явном виде не приводится. Масштаб графика уменьшен для лучшего общего обзора. Расположение на функции ПКХ всех почвенно-климатических ареалов за исключением песков пустынь (выходят далеко за пределы графика) обозначено зеленым цветом и отдельно ареалов черноземов - черным цветом. Видно, что область черноземов располагается в переходной зоне на перегибе функции. Обе ветви производной от функции ПКХ асимптотически стремятся к строго прямолинейным зависимостям.

Диапазоны почвенно-климатических ареалов сильно перекрывают друг друга. Это является следствием того, что относительные переменные - почвенно-климатические гидротермические коэффициенты, рассмотренные в настоящей работе, отражают только самые общие, универсальные почвенно-климатические закономерности. За их рамками остается большое количество не учтенных факторов. Однако возможно воспользоваться процедурой усреднения параметров каждого почвенно-климатического ареала и проанализировать расположения их проекций друг относительно друга на кривой ПКХ - в линейном представлении. Эти результаты представлены на (рис.8).

Основная закономерность, ярко проявившаяся на этом "одномерном" рисунке, заключается в том, что черноземный почвенно-климатический ареал (номер 6) естественным образом разделяет почвы аридного педокосма (к ним относятся ареалы с номерами 1, 2, 3, 4, 5, 15) от почв гумидного царства (ареалы с номерами 7, 8, 9, 10, 11, 12а, 12в, 13, 14, 16). Новизна здесь заключается не в самом разделении ареалов, а в методе, с помощью которого эта группировка произведена. То, что модель подтверждает совершенно естественные представления почвоведов, свидетельствует о правильности исходной схематизации описываемого явления.

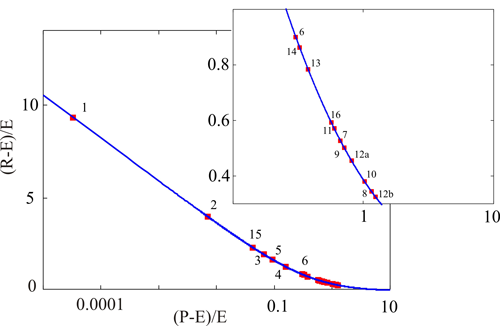
Рисунок 8. Расположение средних значений почвенно-гидротермических коэффициентов для почвенно-климатических ареалов на графике уравнения ПКХ. Номера почвенно-климатических ареалов соответствуют нумерации рисунка 2. Врезка в верхнем правом углу показывает нижнюю правую часть графика в увеличенном масштабе. Область черноземов (номер 6) отделяет аридные почвы (1, 2, 3, 4, 5, 15) от гумидных (7 - 16). Видно, что некоторые почвы стягиваются в группы, примерно соответствующие гидрорядам В. Р. Волобуева. Отметим, что относительное расположение почвенных групп примерно соответствует пропорции золотого сечения.

Обратим внимание на стягивание некоторых почв в близкие группы. Сопоставление этих групп, с гидротермической системой В. Р. Волобуева, позволяет отнести их к соответствующим гидрорядам. Однако раскрытие их тонкой структуры, в рамках принятого в настоящей работе приближения невозможно. Для этого необходимо перейти от относительных величин к абсолютным, и выбрать в качестве новых переменных - гидро- и терморяды. Забегая вперед, отметим, что в этом случае, между рядами можно установить взаимосвязи, дополняющие ПКХ.  В силу ограниченности объема статьи, мы предполагаем сделать это в отдельной работе.

Новый теоретический подход, рассмотренный в настоящей работе и новые результаты, получены в результате применения фундаментального принципа симметрии, в форме анализа размерности, к задаче установления зависимости характера почвенного покрова от гидротермических условий. В результате оказалось возможным более полно учесть специфику взаимосвязей между различными факторами почвообразования. Отметим, что посредством учета зависимости испарения почвенной влаги от гранулометрического состава почв, от их расположения на катене и других факторов, существует возможность дальнейшего обобщения рассмотренного подхода.

В заключении подчеркнем, что нахождение моделей и границ их применимости, адекватных каждому уровню познания, является основным содержанием науки. Хотя пределов уточнения моделей практически не существует, всегда есть разумный предел в стремлении более глубоко познать природу. С этих позиций следует относится и к модели ПКХ, описанной в настоящей работе. В определенном отношении она является обобщением традиционных методов, но существует и более общий взгляд на почвенные закономерности, с позиций которого модель все равно является сильно идеализированной.

1. Ограниченная применимость традиционных гидротермических коэффициентов - радиационного индекса сухости Будыко и коэффициента увлажнения Высоцкого - Иванова, при характеристике особенностей распределения почв в зависимости от гидротермических условий, является следствием использования в их определениях не полного набора переменных, существенных для процессов тепло-влагообмена почв с атмосферой. При количественном описании почвенных закономерностей, использование в качестве эталонов различных состояний свободной влаги, чрезмерно огрубляет (идеализирует) физическую картину этих явлений.

2. Условием логической совместимости традиционных коэффициентов, при их одновременном использовании с уравнением испарения почвенной влаги, для более полной характеристики гидротермических условий почвообразования, является использование в определениях обоих коэффициентах, в качестве общего масштаба - функции испарения почвенной (а не свободной) влаги. Такие определения более адекватно отражают специфику неразрывного взаимодействия процессов тепло-влагообмена почвы и климата, с одновременным учетом свойств почвенного субстрата.

3. Определены два новых понятия - критерия подобия, играющих роль новых, более общих почвенно-климатических коэффициентов. Показано, что связь новых коэффициентов и традиционных носит асимптотический характер. Тем самым установлен факт не универсальности традиционных гидротермических коэффициентов и обозначены границы их применимости.

4. Из уравнения испарения почвенной влаги М. И. Будыко, с использованием новых почвенно-климатических коэффициентов, выведено уравнение, остающееся инвариантным при любых изменениях переменных. Это универсальное уравнение предложено называть "почвенно-климатической характеристикой" (ПКХ), поскольку оно в более общем виде, по сравнению с традиционными коэффициентами, отражает специфику взаимодействия тепла, влаги и почвенного субстрата в почвообразовательном процессе.

5. Универсальность уравнения ПКХ позволяет рассматривать его как предпосылку простейшей феноменологической теории, из которой логически следует:

а) вывод традиционных климатических гидротермических коэффициентов как асимптотических пределов новых почвенно-климатических коэффициентов;

б) теоретическое предсказание существования двух областей автомодельности общего уравнения ПКХ, характеризующихся различными симметриями подобия. С этими областями естественно связываются группы почв аридного и гумидного педокосмов;

в) доказательство невозможности теоретической группировки почв в случае использования традиционных климатических гидротермических коэффициентов;

г) возможность приближенного рассмотрения уравнения ПКХ как суперпозиции двух  составляющих (аридной и гумидной) с нелинейными весовыми коэффициентами. В таком приближении каждая почва характеризуется различным вкладом аридной и гумидной составляющих. Диапазон увлажнения, с приблизительно равным вкладом составляющих, естественно интерпретируется как педокосм почв сбалансированного (или переходного) увлажнения. Такой подход дает возможность провести группировку почв, основанную на принципах подобия и показывает принципиальную роль в исследовании как точных методов, так и приближенных.

6. Показано, что причина ограниченной применимости количественного подхода В. Р. Волобуева в экологии почв, основанного на энергетических представлениях, связана не только с тем, что в коэффициенте увлажнения используются усредненные значения отдельных факторов почвообразования, но и с тем, что в качестве системы отсчета для них принимаются состояния почв только с высоким уровнем увлажнения.

Финансовая поддержка

Работа выполнена при финансовой поддержке Министерства высшего образования и науки Российской Федерации по государственному заданию Института почвоведения и агрохимии СО РАН, г. Новосибирск.

1. Волобуев В.Р. О почвенно-климатических ареалах // Почвоведение. 1945. № С. 3–16.
2. Волобуев В. Р. Почвы и климат. Баку: Изд. Акад. наук Азерб. ССР., 1953. 320 с.
3. Волобуев В. Р. Климатические условия и почвы // Почвоведение. 1956. № 4. С. 24–37.
4. Волобуев В. Р.Экология почв. Баку: Изд-во АН Азер. ССР, 1963.
5. Волобуев В. Р. Система почв мира. Баку: ЭЛМ, 1973. 308 с.
6. Волобуев В. Р. Введение в энергетику почвообразования. М.: Наука, 1974. 128 с.
7. Глазовская М. А. Общее почвоведение и география почв. М. Высшая школа. 1981. 400 с.
8. Гухман А. А. Введение в теорию подобия. М.: Высшая школа, 1973. 296 с.
9. Добровольский Г. В., Урусевич И. С. География почв. М. Изд-во МГУ. 2004. 460 С.
10. Ковда В.А. Основы учения о почвах. М.: Наука, 1973. Т. 1. 448 с.
11. Кутателадзе С. С. Анализ подобия в теплофизике. Новосибирск, Наука Сиб. отд.,1982. 280 с.
12. Левич А.П. Метаболическое время естественных систем //Системные исследования. М.: Наука, 1989. С. 304–325.
13. Планк М. Единство физической картины мира. М.: Наука, 1966. 288 с.
14. Реймерс Н. Ф. Природопользование. Словарь-справочник. М.: Мысль, 1990. 637 с.
15. Седов Л. И. Методы подобия и размерности в механике. М. Наука. 1981. 448 с.
16. Сена Л.А. Единицы физических величин и их размерности. М.: Наука, 1988, 309 с.
17. Соколов И. А. Теоретические проблемы генетического почвоведения. Новосибирск: "Гуманитарные технологии", 2004. 288 с.
18. Хильми Г. Ф. Методологические вопросы наук о биосфере // Материалистическая диалектика и методы естественных наук. М.: Наука, 1968. 489–497 с.
19. Чичулин А. В., Елизарова Т. Н. Эвристический характер принципа подобия в физике почв // Сибирский экологический журнал. 2004. Т.11. № 3. С. 433–443.
20. Чичулин А.В. Дитц Л.Ю. Инвариантная форма влажностной характеристики почв // Материалы V Всероссийского съезда общества почвоведов им. В. В. Докучаева. 2008. Тезисы докладов. Ростов-на-Дону: Ростиздат. С. 506.
21. Чичулин А.В. Пространственно-временные симметрии физических явлений в почвах // Сибирский экологический журнал. 2010. Т.17. № 3. С.389–398.
22. Чичулин А.В., Шапорина Н.А. Методологическое значение анализа размерности в экологии почв // Международный журнал прикладных и фундаментальных исследований. 2016. № 12. Вып.8. С.1474–1478.

Чичулин Александр Валентинович – кандидат биологических наук, старший научный сотрудник лаборатории почвенно-физических процессов Института почвоведения и агрохимии СО РАН (Новосибирск, Россия); chichulin@issa-siberia.ru

Автор прочитал и одобрил окончательный вариант рукописи

Статья доступна по лицензии Creative Commons Attribution 4.0 License

METHODOLOGICAL ANALYSIS OF THE CONCEPTUAL FRAMEWORK IN SOIL ECOLOGY

A. V. Chichulin

Address: Institute of Soil Science and Agrochemistry, Siberian Branch of the Russian Academy of Sciences, Novosibirsk, Russia

A methodological analysis is carried out and the reasons for the limited applicability in solving a number of problems in soil ecology of traditional climatic hydrothermal coefficients — the radiation index of Budyko dryness and the Vysotsky-Ivanov wetting coefficient — are clarified. Based on the analysis of the dimension applied to the problem of the dependence of the nature of the soil cover on hydrothermal conditions, new concepts are introduced - dimensionless similarity criteria, which play the role of soil-climate coefficients, which have a wider range of epistemological accuracy compared to traditional ones. It is shown that the relationship between traditional climatic and new soil-climatic hydrothermal coefficients is asymptotic. Using the empirical equation of M. I. Budyko for evaporation of soil moisture and soil-climatic coefficients, a new physico-theoretical approach is developed and the equation of "soil-climatic characteristics" (PCC) is taken into account, taking into account the combined influence of climatic properties (through long-term average the values of the radiation balance R and precipitation P) and the properties of the soil substrate (through the evaporation of soil moisture E (R, P)) on the features of the soil formation process. It is shown that, in contrast to the traditional approach, which organizes soil properties on an empirical climatic basis, the new approach has the ability to theoretically predict a number of soil patterns, in particular, grouping soils into arid, humid, and balanced pedocosms.

Key words: soil ecology; principles of symmetry; principle of complementarity; hydrothermal coefficients; idealization; mathematical model

How to cite: Chichulin A.V. Methodological analysis of the conceptual framework in soil ecology // The Journal of Soil and Environment. 2019. 2(3). e89. 10.31251/pos.v2i3.89 (in Russian with English abstract).

References

1. Volobuev V.R. On Soil-Climatic Areas, Pochvovedenie, 1945, No.1, p.3-16. (in Russian)
2. Volobuev V.R. Soils and climate. Baku: Acad. Sciences Azerb. SSR., 1953. 320 p. (in Russian)
3. Volobuev V.R. Climatic conditions and soils, Pochvovedenie, 1956, No. 4, p.24-37. (in Russian)
4. Volobuev V.R. Soil system of the world. Baku: ELM Publ., 1973. 308 p. (in Russian)
5. Volobuev V.R. Ecology of soils. Baku: Publishing House of the Academy of Sciences of Azerbaijan. SSR, 1963. (in Russian)
6. Volobuev V.R. Introduction to the energy of soil formation. Moscow: Nauka Publ., 1974. 128 p. (in Russian)
7. Glazovskaya M. A. General soil science and soil geography. Moscow: High School Publ., 1981. 400 p. (in Russian)
8. Gukhman A.A. Introduction to the theory of similarity. Moscow: Higher School Publ., 1973. 296 p. (in Russian)
9. Dobrovolsky G.V., Urusevich I.S. Geography of soils. Moscow: Publishing House of Moscow State University. 2004. 460 p. (in Russian)
10. Kovda V.A. Fundamentals of the doctrine of soils. Moscow: Nauka Publ., 1973.V. 1. 448 p. (in Russian)
11. Kutateladze S. S. Similarity analysis in thermal physics. Novosibirsk: Nauka Publ., 1982. 280 p. (in Russian)
12. Levich A.P. Metabolic time of natural systems. In book: System studies. Moscow: Nauka Publ., 1989, p. 304-325. (in Russian)
13. Planck M. Unity of the physical picture of the world. Moscow: Nauka Publ., 1966. 288 p. (in Russian)
14. Reimers N.F. Nature Management. Dictionary.  Moscow: Mysl’ Publ., 1990. 637 p. (in Russian)
15. Sedov L.I. Methods of similarity and dimension in mechanics. Moscow: Nauka Publ., 1981. 448 p. (in Russian)
16. Sena L.A. Units of physical quantities and their dimensions. Moscow: Nauka Publ., 1988. 309 p. (in Russian)
17. Sokolov I. A. Theoretical Problems of Genetic Soil Science. Novosibirsk: Humanitarian Technologies Publ., 2004. 288 p. (in Russian)
18. Hilmi G.F. Methodological issues of the biosphere sciences. In book: Materialistic dialectics and methods of natural sciences. Moscow: Nauka Publ., 1968. 489-497 p. (in Russian)
19. Chichulin A. V., Elizarova T. N. Heuristic Character of the Similarity Principle in the Physics of Soil, Sibirskii ecologicheskii zhurnal, 2004. 11(3), p. 433–443. (in Russian)
20. Chichulin A. V. Ditz L. Yu. Invariant form of soil moisture characteristicsю In book: Abstracts of the V^th Russian Congress of the Society of Soil Scientists named after V.V. Dokuchaev. 2008. Rostov-na-Donu: Rosizdat Publ., p. 506. (in Russian)
21. Chichulin A. V. Spatial-temporal symmetries of physical phenomena in soils, Contemporary problems of ecology, 2010, 3(3), p.272–278. CrossRef
22. Chichulin A.V., Shaporina N. A. Methodological significance of dimensional analysis in soil ecology, International Journal of Applied and Basic Research, 2016, 12(8), p.1474-1478. (in Russian).

Received 01 December 2019; accepted 19 December 2019; published 19 December 2019

About the author:

Chichulin Alexander V. – – Candidate of Biological Sciences, Senior Researcher in the Laboratory of Soil Physical Processes in the Institute of Soil Science and Agrochemistry of the Siberian Branch of the Russian Academy of Sciences (Novosibirsk, Russia); chichulin@issa-siberia.ru

The author read and approved the final manuscript

The article is available under Creative Commons Attribution 4.0 License